不规则图形面积的计算.docx

不规则图形面积的计算.docx

《不规则图形面积的计算.docx》由会员分享，可在线阅读，更多相关《不规则图形面积的计算.docx（11页珍藏版）》请在冰豆网上搜索。

不规则图形面积的计算

第一讲不规则图形面积的计算

（一）

我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形，一般称为基本图形或规则图形，它们的面积及周长都有相应的公式直接计算。

实际问题中，有些图形不是以基本图形的形状出现，而是由一些基本图形组合、拼凑成的，它们的面积及周长无法应用公式直接计算。

一般我们称这样的图形为不规则图形。

那么，不规则图形的面积及周长怎样去计算呢？

我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系，问题就能解决了。

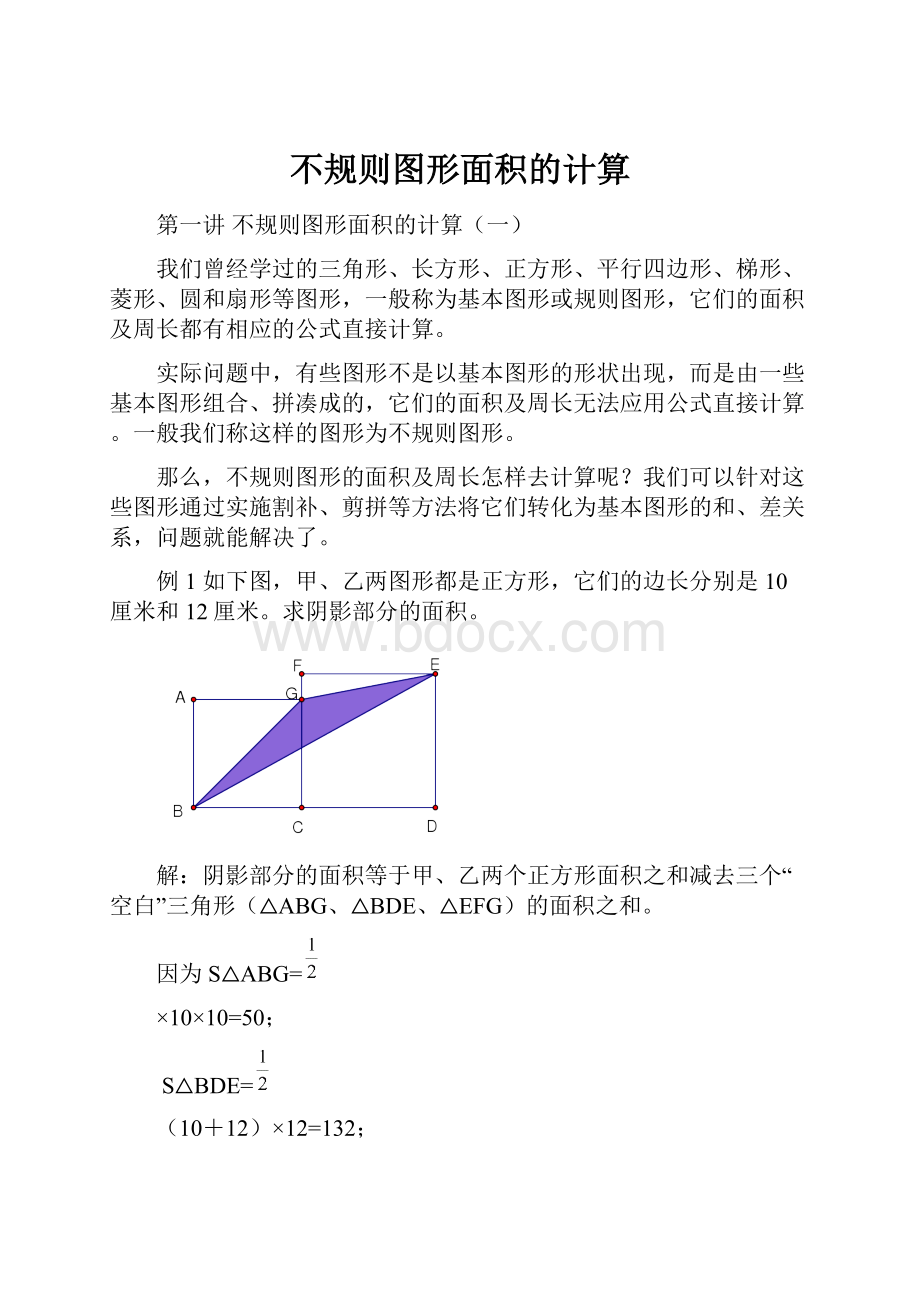
例1如下图，甲、乙两图形都是正方形，它们的边长分别是10厘米和12厘米。

求阴影部分的面积。

解：

阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形（△ABG、△BDE、△EFG）的面积之和。

因为S△ABG=

×10×10=50；

S△BDE=

（10＋12）×12=132；

S△EFG=

（12－10）×12=12。

又因为S甲＋S乙=12×12＋10×10=244，

所以阴影部分面积=244－（50＋132＋12）=50（平方厘米）

例2如下图，正方形ABCD的边长为6厘米，△ABE、

△ADF与四边形AECF的面积彼此相等，求三角形AEF的面积。

解：

因为△ABE、△ADF与四边形AECF的面积彼此相等，所以四边形AECF的面积与△ABE、△ADF的面积都等于正方形ABCD面积的三分之一。

也就是：

S四边形AECF=S△ABE=S△ADF=

×6×6=12。

在△ABE中，因为AB=6，所以BE=4，同理DF=4，因此，CE=CF=2，所以△ECF的面积为2×2÷2=2。

所以S△AEF=S四边形AECF－S△ECF=12－2=10（平方厘米）。

例3：

两块等腰直角三角形的三角板，直角边分别是10厘米和6厘米。

如下图那样重合。

求重合部分（阴影部分）的面积。

解：

在等腰直角三角形ABC中，

∵AB=10

∴S△ABC=

×10×10=50

又∵S△ABG=

S△ABC=

×50=25，

∵EF=BF=AB－AF=10－6=4，

∴S△BEF=

×4×4=8，

∴阴影部分面积=S△ABG－S△BEF=25－8=17（平方厘米）。

例4：

如下图，A为△CDE的DE边上中点，BC=

CD，若

△ABC（阴影部分）面积为5平方厘米，求△ABD及△ACE的面积。

解：

取BD中点F，连结AF。

因为△ADF、△ABF和△ABC等底等高，所以它们的面积相等，都等于5平方厘米。

所以△ACD的面积等于15平方厘，△ABD的面积等于10平方厘米。

又由于△ACE与△ACD等底等高，所以△ACE的面积是15平方厘米。

例5：

如下图，在正方形ABCD中，三角形ABE的面积是8平方厘米，它是三角形DEC的面积的

。

求正方形ABCD的面积。

解：

过E作BC的垂线交AD于F。

在矩形ABEF中，AE是对角线，所以S△ABE=S△AEF=8。

在矩形CDFE中DE是对角线，所以S△ECD=S△EDF。

因此，正方形面积=8×2＋8÷

×2=36（平方厘米）。

例6：

已知S△ABC=1，AE=ED，BD=

BC，求阴影部分的面积。

解：

连结DF。

∵AE=ED，∴S△AEF=S△DEF；S△ABE=S△BED，

∴S阴影=S△ABF=S△BFD。

∵BD=

BC，

∴S△BFD=

S△BCF=

（1－S△ABF），

∴S△ABF=

（1－S△ABF），∴S△ABF=

。

∴阴影部分面积为

。

例7：

正方形ABCD的边长是4厘米，CG=3厘米，矩形DEFG的长DG为5厘米，求它的宽DE等于多少厘米？

解：

连结AG，自A作AH垂直DG于H，在△ADG中，AD=4，DC=4（AD上的高）。

∴S△AGD=4×4÷2=8，又DG=5，

∴S△AGD=AH×DG÷2=

∴AH=8×2÷5=3.2（厘米），∴DE=3.2（厘米）。

例8：

梯形ABCD的面积是45平方米，高6米，△AED的面积是5平方米，BC=10米，求阴影部分的面积。

解：

∵梯形面积=（上底＋下底）×高÷2

即45=（AD＋BC）×6÷2

45=（AD＋10）×6÷2

∴AD=45×2÷6－10=5米。

又S△ADE=

×AD×高，即5=

×5×高，

∴△ADE的高是2米，△EBC的高等于梯形的高减去△ADE的高，即6－2=4米。

∴S△BEC=

×BC×4=

×10×4=20（平方米）。

例9：

如图，四边形ABCD和DEFG都是平行四边形，证明它们的面积相等。

证明：

连结CE，平行四边形ABCD的面积等于△CDE面积的2倍，而平行四边形DEFG的面积也是△CDE面积的2倍。

所以，平行四边形ABCD的面积与平行四边形DEFG的面积相等。

习题一

一、填空题（求下列各图中阴影部分的面积）：

二、解答题：

1．如右图，ABCD为长方形，AB=10厘米，BC=6厘米，E、F分别为AB、AD中点，且FG=2GE。

求阴影部分的面积。

2．如图，正方形ABCD与正方形DEFG的边长分别为12厘米和6厘米。

求四边形CMGN（阴影部分）的面积。

3．正方形ABCD的边长为5厘米，△CEF的面积比△ADF的面积大5平方厘米。

求CE的长。

4．如下图，已知CF=2DF，DE=EA，三角形BCF的面积为2，四边形BEDF的面积为4。

求三角形ABE的面积。

5．直角梯形ABCD的上底BC=10厘米，下底AD=14厘米，高CD=5厘米。

又三角形ABF、三角形BCE和四边形BEDF的面积相等。

求三角形DEF的面积。

6．如下图，四个一样大的长方形和一个小的正方形拼成一个大正方形，其中大、小正方形的面积分别是64平方米和9平方米。

求长方形的长、宽各是多少？

7．如下图，有一三角形纸片沿虚线折叠得到右图，它的面积与原三角形面积之比为2：

3，已知阴影部分的面积为5平方厘米，求原三角形面积。

8．如下图，平行四边形ABCD的边长BC=10，直角三角形BCE的直角边EC长8，已知阴影部分的面积比三角形EFG的面积大10。

求CF的长。