 流体流动习题.docx
流体流动习题.docx
- 文档编号:11276729
- 上传时间:2023-02-26
- 格式:DOCX
- 页数:9
- 大小:144.56KB
流体流动习题.docx
《流体流动习题.docx》由会员分享,可在线阅读,更多相关《流体流动习题.docx(9页珍藏版)》请在冰豆网上搜索。
流体流动习题
流体流动习题
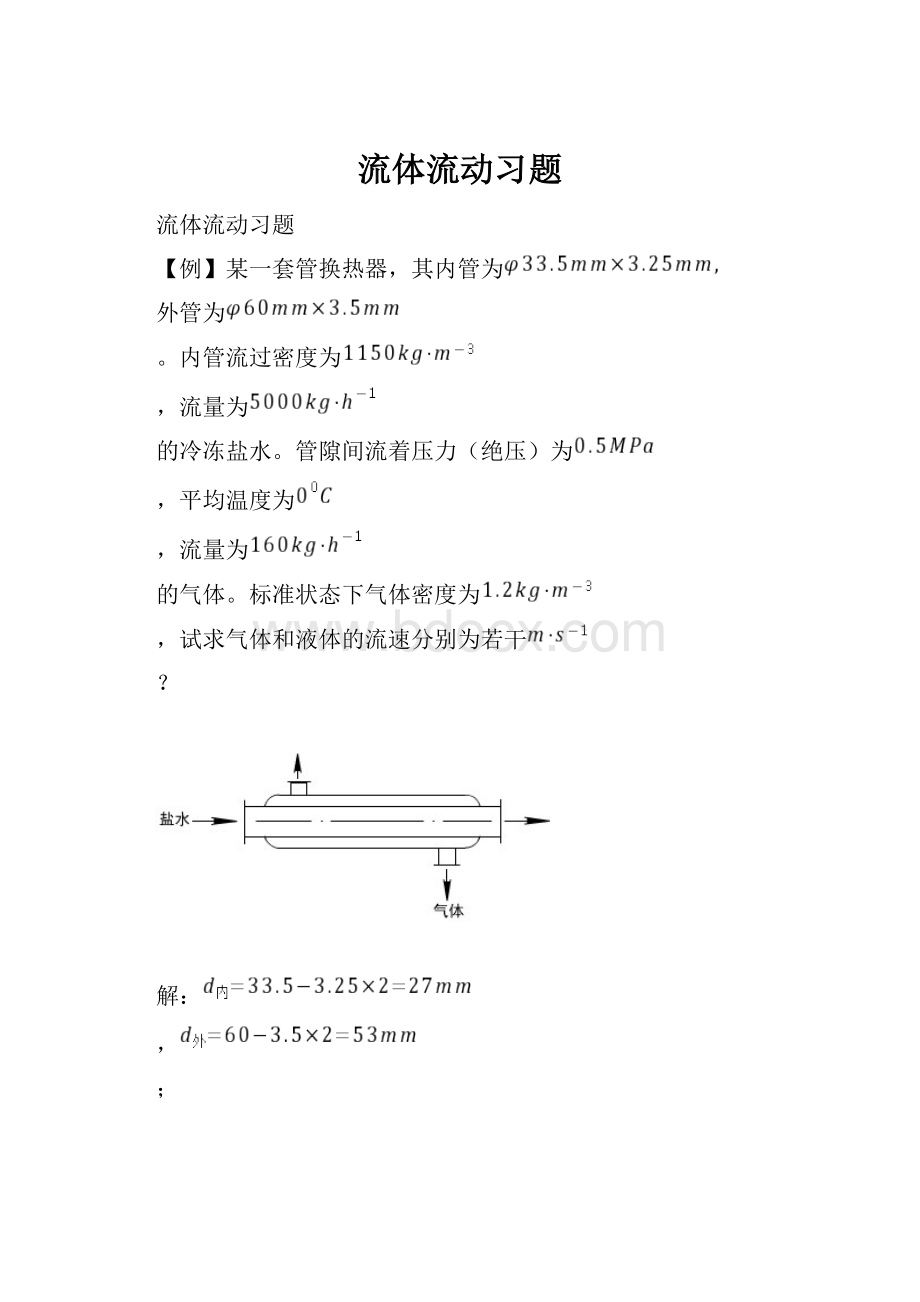
【例】某一套管换热器,其内管为
外管为
。
内管流过密度为
,流量为
的冷冻盐水。
管隙间流着压力(绝压)为
,平均温度为
,流量为
的气体。
标准状态下气体密度为
,试求气体和液体的流速分别为若干
?
解:
,
;
对液体:
;
对气体:
,
,
。
【例】水在本题附图所示的虹吸管内作定态流动,管路直径没有变化,水流经管路的能量损失可以忽略不计,试计算管内截面2-2'、3-3'、4-4'和5-5'处的压强。
大气压强为1.0133×105Pa。
图中所标注的尺寸均以mm计。
(g=9.81m/s-2)
【例】水在本题附图所示的虹吸管内作定态流动,管路直径没有变化,水流经管路的能量损失可以忽略不计,试计算管内截面2-2'、3-3'、4-4'和5-5'处的压强。
大气压强为1.0133×105Pa。
图中所标注的尺寸均以mm计。
(g=9.81m/s-2)
解:
为计算管内各截面的压强,应首先计算管内水的流速。
先在贮槽水面1-1'及管子出口内侧截面6-6'间列柏努利方程式,并以截面6-6'为基准水平面。
由于管路的能量损失忽略不计,即
=0,故柏努利方程式可写为
式中Z1=1mZ6=0p1=0(表压)p6=0(表压)u1≈0
将上列数值代入上式,并简化得
解得u6=4.43m/s
由于管路直径无变化,则管路各截面积相等。
根据连续性方程式知Vs=Au=常数,故管内各截面的流速不变,即
u2=u3=u4=u5=u6=4.43m/s
则
因流动系统的能量损失可忽略不计,故水可视为理想流体,则系统内各截面上流体的总机械能E相等,即
总机械能可以用系统内任何截面去计算,但根据本题条件,以贮槽水面1-1'处的总机械能计算较为简便。
现取截面2-2'为基准水平面,则上式中Z=2m,p=101330Pa,u≈0,所以总机械能为
计算各截面的压强时,亦应以截面2-2'为基准水平面,则Z2=0,Z3=3m,Z4=3.5m,Z5=3m。
(1)截面2-2'的压强
(2)截面3-3'的压强
(3)截面4-4'的压强
(4)截面5-5'的压强
从以上结果可以看出,压强不断变化,这是位能与静压强反复转换的结果。
【例】如附图所示,某厂利用喷射泵输送氨。
管中稀氨水的质量流量为1×104kg/h,密度为1000kg/m3,入口处的表压为147kPa。
管道的内径为53mm,喷嘴出口处内径为13mm,喷嘴能量损失可忽略不计,试求喷嘴出口处的压力。
【例】如附图所示,某厂利用喷射泵输送氨。
管中稀氨水的质量流量为1×104kg/h,密度为1000kg/m3,入口处的表压为147kPa。
管道的内径为53mm,喷嘴出口处内径为13mm,喷嘴能量损失可忽略不计,试求喷嘴出口处的压力。
解:
取稀氨水入口为1-1′截面,喷嘴出口为2-2′截面,管中心线为基准水平面。
在1-1′和2-2′截面间列柏努利方程
其中:
z1=0;p1=147×103Pa(表压);
m/s
z2=0;喷嘴出口速度u2可直接计算或由连续性方程计算
m/s
We=0;ΣWf=0
将以上各值代入上式
解得p2=-71.45kPa(表压)
即喷嘴出口处的真空度为71.45kPa。
喷射泵是利用流体流动时静压能与动能的转换原理进行吸、送流体的设备。
当一种流体经过喷嘴时,由于喷嘴的截面积比管道的截面积小得多,流体流过喷嘴时速度迅速增大,使该处的静压力急速减小,造成真空,从而可将支管中的另一种流体吸入,二者混合后在扩大管中速度逐渐降低,压力随之升高,最后将混合流体送出。
【例】料液自高位槽流入精馏塔,如附图所示。
塔内压强为1.96×104Pa(表压),输送管道为φ36×2mm无缝钢管,管长8m。
管路中装有90°标准弯头两个,180°回弯头一个,球心阀(全开)一个。
为使料液以3m3/h的流量流入塔中,问高位槽应安置多高?
(即位差Z应为多少米)。
料液在操作温度下的物性:
密度ρ=861kg/m3;粘度μ=0.643×10-3Pa·s。
【例】料液自高位槽流入精馏塔,如附图所示。
塔内压强为1.96×104Pa(表压),输送管道为φ36×2mm无缝钢管,管长8m。
管路中装有90°标准弯头两个,180°回弯头一个,球心阀(全开)一个。
为使料液以3m3/h的流量流入塔中,问高位槽应安置多高?
(即位差Z应为多少米)。
料液在操作温度下的物性:
密度ρ=861kg/m3;粘度μ=0.643×10-3Pa·s。
解:
取管出口处的水平面作为基准面。
在高位槽液面1-1与管出口截面2-2间列柏努利方程
式中Z1=ZZ2=0p1=0(表压)
u1≈0p2=1.96×104Pa
阻力损失
取管壁绝对粗糙度ε=0.3mm,则:
由图1-23查得λ=0.039
局部阻力系数由表1-4查得为
进口突然缩小(入管口)ζ=0.5
90°标准弯头ζ=0.75
180°回弯头ζ=1.5
球心阀(全开)ζ=6.4
故
=10.6J/kg
所求位差
截面2-2也可取在管出口外端,此时料液流入塔内,速度u2为零。
但局部阻力应计入突然扩大(流入大容器的出口)损失ζ=1,故两种计算方法结果相同。
- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 流体 流动 习题
 冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。


 《JAVA编程基础》课程标准软件16级.docx
《JAVA编程基础》课程标准软件16级.docx
