旋转专题复习专题.docx

旋转专题复习专题.docx

《旋转专题复习专题.docx》由会员分享，可在线阅读，更多相关《旋转专题复习专题.docx（44页珍藏版）》请在冰豆网上搜索。

旋转专题复习专题

旋转专题复习专题

一•选择题（共15小题）

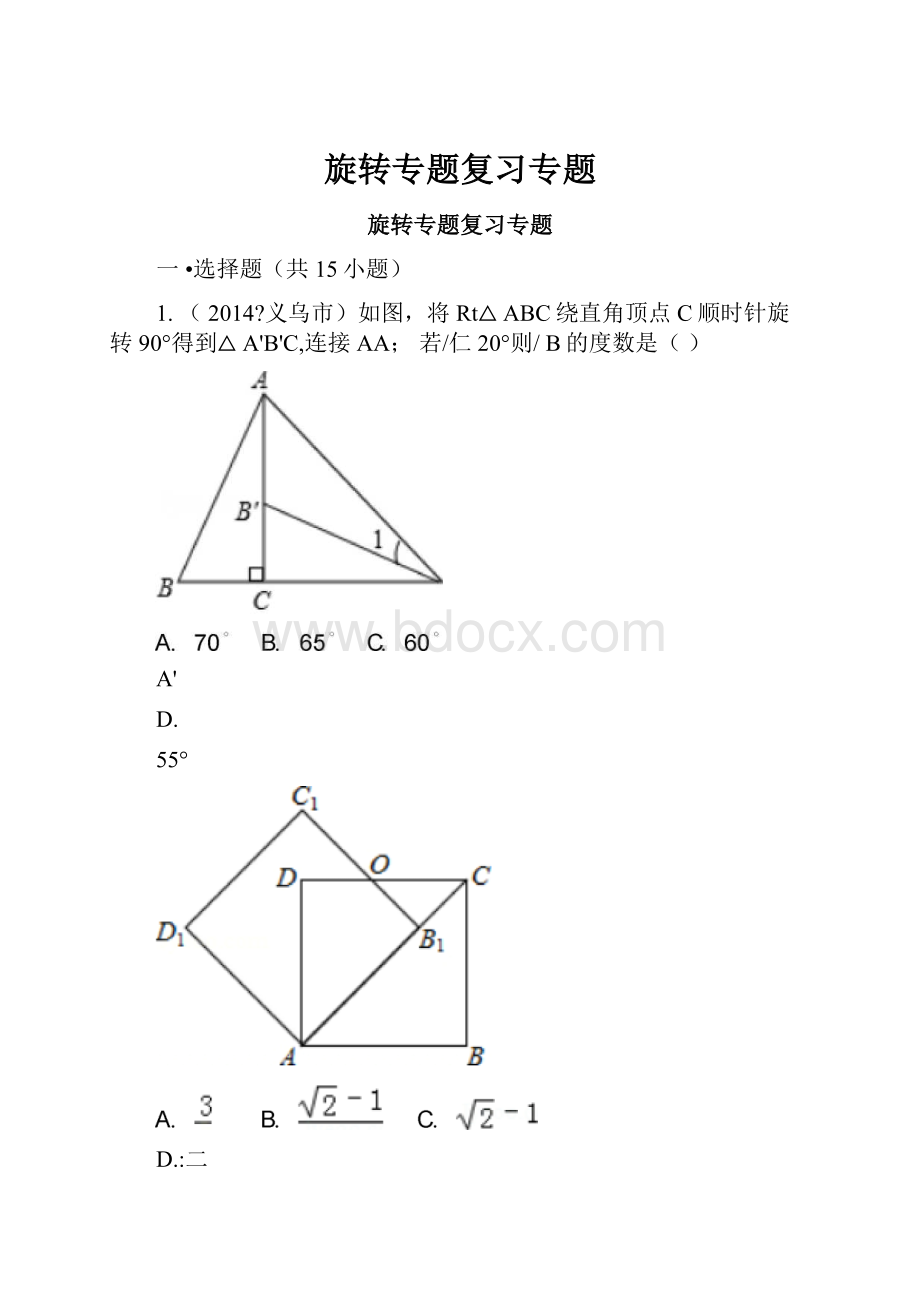
1.（2014?

义乌市）如图，将Rt△ABC绕直角顶点C顺时针旋转90°得到△A'B'C,连接AA；若/仁20°则/B的度数是（）

A'

D.

55°

D.:

二

正方形的性质.

4【考点】【专题】【分析】

2

旋转的性质；

几何图形问题.

连接AG,AO根据四边形

【考点】旋转的性质.

【专题】几何图形问题.

【分析】根据旋转的性质可得AC=AC,然后判断出△ACA是等腰直角三角形，根据等腰直角

三角形的性质可得/CAA=45°再根据三角形的一个外角等于与它不相邻的两个内角的和求出/A'B'C,然后根据旋转的性质可得/B=ZAB'C.

【解答】解：

IRt△ABC绕直角顶点C顺时针旋转90°得到△A'B'C,

•••AC=AC,

•••△ACA是等腰直角三角形，

•••/CAA=45°

•••/ABC=Z1+ZCAA=20°+45°=65°,

由旋转的性质得/B=ZA'B'C=65°.

故选：

B.

【点评】本题考查了旋转的性质，等腰直角三角形的判定与性质，三角形的一个外角等于与

它不相邻的两个内角的和的性质，熟记各性质并准确识图是解题的关键.

3.（2014?

大庆）如图，边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形ABCiDi,边BC与CD交于点O,则四边形ABOD的面积是（）

/DAB=45°推出A、D、C,三点共线,根据三角形的面积计算即可.

ABGD是正方形，得出/GAB|=/ACB=45°求出

在Rt△GDlA中，由勾股定理求出AC,进而求出DC=OD

【解答】解：

连接AG,

•••四边形ABGD是正方形，

•••/GAB=1>90°45°/AGBi,

2

•••边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形ABGiDi,•••/BiAB=45,

•••/DAB=90°-45°45°

•AGi过D点，即ADG三点共线，

•••正方形ABCD勺边长是1,

•四边形ABCD的边长是1,

在Rt△GiDlA中，由勾股定理得：

AG=/[2+]2=应,

则DG也-1,

•••/AGB1=45°/G1DO=90,

•••/GOD=45=/DGO,

•DG=OD=/^-1,

•SAADO=XOD*AD=^,

22

•四边形ABOD勺面积是=2也一1=伍-1,

2

【点评】本题考查了正方形性质，勾股定理等知识点，主要考查学生运用性质进行计算的能力，题目比较好，但有一定的难度.

4.（2014?

苏州）如图，△AOB为等腰三角形，顶点A的坐标（2,-■）,底边OB在x轴上.将

△AOB绕点B按顺时针方向旋转一定角度后得△A'OB,点A的对应点A在x轴上，则点O'的

「，「）D.（"厂）

【考点】坐标与图形变化-旋转.

【专题】计算题；压轴题.

【分析】过点A作ACL0B于C,过点0作0D丄A'B于D,根据点A的坐标求出OGAC,再利用勾股定理列式计算求出0A根据等腰三角形三线合一的性质求出0B根据旋转的性质

可得B0=0B/A'B0=/AB0然后解直角三角形求出0'DBD,再求出0D然后写出点0'的坐标即可.

【解答】解：

如图，过点A作ACL0B于C,过点0作0'DLA'B于D,

A（2,7）,_

二0C=2AC=Jj,

由勾股定理得,0A=L「_=「r-=3，

•••△A0B为等腰三角形，0B是底边，

/•0B=20C=22=4,

由旋转的性质得，B0=0B=4/AB0=/AB0

O'D=4X,

33

BD=4X=■',

33

•••0D=0B+BD=4+=…",

33

•••点o'的坐标为（戲,上一）.

33

故选：

C.

A.30°

【考点】

【专题】

6.（2014?

遂宁）如图，在Rt△ABC中，/ACB=90°/ABC=30°将厶ABC绕点C顺时针旋转至厶A'B'C,使得点A"恰好落在AB上，则旋转角度为（）

Br

B.60°C.90°D.150旋转的性质.

几何图形问题.

【分析】根据直角三角形两锐角互余求出/A=60°根据旋转的性质可得AC=AC，然后判断

出AA'AC是等边三角形，根据等边三角形的性质求出/ACA=60°然后根据旋转角的定义解

答即可.

【解答】解：

•••/ACB=90,/ABC=30,

•••/A=90°-30°60°

•••△ABC绕点C顺时针旋转至△A'B'C时点A恰好落在AB上，

•AC=AC,

•••△A'AC是等边三角形，

•••/ACA=60°

•••旋转角为60°

故选：

B.

【点评】本题考查了旋转的性质，直角三角形两锐角互余，等边三角形的判定与性质，熟记

各性质并准确识图是解题的关键.

7.（2014?

遵义）如图，已知△ABC中，/C=90°,AC=BC羽，将△ABC绕点A顺时针方向旋转60°到△ABC的位置，连接CB,贝UCB的长为（）

2

C.7-1

【考点】旋转的性质.

D.1

【分析】连接BB；根据旋转的性质可得AB=AB,判断出△ABB'是等边三角形，根据等边三角形的三条边都相等可得AB=BB,然后利用边边边”证明△ABOABBC全等，根据全等三角形对应角相等可得/ABC=ZBBC',延长BC交AB于D,根据等边三角形的性质可得BD丄AB',利用勾股定理列式求出AB,然后根据等边三角形的性质和等腰直角三角形的性质求出BD

C'D,然后根据BC=BD-C'D计算即可得解.

【解答】解：

如图，连接BB',

•••△ABC绕点A顺时针方向旋转60。

得到△ABC,

•AB=AB,ZBAB=60°

•△ABB是等边三角形，

•AB=BB,

在厶ABMMB'BC中,

”虻丿二Cz,

二EC'

•△ABC^ABBC（（SSS,

•••/ABC=ZBBC；

延长BC交AB于D,

贝UBD丄AB,

•••/C=90°,AC=BC==,•••AB=「.-：

：

'=2,

BD=2xD=-

2

C'D=X2=1,

2

•••BC=BD-CD=二-1.

故选：

C.

【点评】本题考查了旋转的性质，全等三角形的判定与性质，等边三角形的判定与性质，等腰直角三角形的性质，作辅助线构造出全等三角形并求出BC在等边三角形的高上是解题的关键，也是本题的难点.

&（2014?

泰安）将两个斜边长相等的三角形纸片如图①放置，其中/ACB=/CED=90,

/A=45°/D=30°.把^DCE绕点C顺时针旋转15°得到△DiCE,如图②,连接DB,则/EiDiB

【考点】旋转的性质；全等三角形的判定与性质；等腰直角三角形.

【分析】根据直角三角形两锐角互余求出/DCE=60,旋转的性质可得/BCE=15°然后求出/BCD=45°从而得到/BCD=/A,利用边角边”证明△ABMH△DCB全等，根据全等三角形对应角相等可得/BDC=/ABC=45,再根据/EiDB=/BQC-ZCDE计算即可得解.

【解答】解：

•••/CED=90,/D=30°,

•••/DCE=60,

•••△DCE绕点C顺时针旋转15°.

•••/BCE=15°.

•••/BCD=60°-15°=45°.

•••/BCD=/A,在厶ABC和△D|CB中,

rAC=CB

彳ZBCD^ZA,

AB=CDi

L1

•△ABC^ADCB（SAS,

•••/BDC=/ABC=45,

•••/EiDB=ZBDC-ZCDEi=45°-30°=15°,

故选：

D.

【点评】本题考查了旋转的性质，等腰直角三角形的性质，全等三角形的判定与性质，熟记

性质并求出△ABC和△DiCB全等是解题的关键.

9.（2015?

曲靖）如图，正方形OABC绕着点O逆时针旋转40°得到正方形ODEF连接AF,则/OFA的度数是（）

O

A.15°B.20°C.25°D.30°

【考点】旋转的性质.

【专题】压轴题.

【分析】先根据正方形的性质和旋转的性质得到/AOF的度数，OA=OF再根据等腰三角形

的性质即可求得/OFA的度数.

【解答】解：

•••正方形OABC绕着点O逆时针旋转40°得到正方形ODEF

•••/A0F=90+40°130°OA=OF

•••/OFA=（180°-130°吃=25°.

故选：

C.

【点评】考查了旋转的性质：

①对应点到旋转中心的距离相等.②对应点与旋转中心所连

线段的夹角等于旋转角.③旋转前、后的图形全等.同时考查了正方形的性质和等腰三角形的性质.

10.（2015?

抚顺）如图，将矩形ABCD绕点A旋转至矩形AB'C'D位置，此时AC的中点恰好与D点重合，AB交CD于点E若AB=3则厶AEC的面积为（）

A.3B.1.5C.2■:

D.■:

【考点】旋转的性质.

【专题】计算题；压轴题.

【分析】根据旋转后AC的中点恰好与D点重合，利用旋转的性质得到直角三角形ACD中,

/ACD=30,再由旋转后矩形与已知矩形全等及矩形的性质得到/DAE为30°进而得到

/EAC=ZECA利用等角对等边得到AE=CE设AE=CE=x表示出AD与DE利用勾股定理列出关于x的方程，求出方程的解得到x的值，确定出EC的长，即可求出三角形AEC面积.

【解答】解：

•••旋转后AC的中点恰好与D点重合，即AD=AC=AC

•••在Rt△ACD中，/ACD=30,即/DAC=60,

•••/DAD=60°

•••/DAE=30,

•••/EAC=/ACD=30,

•AE=CE

在Rt△ADE中，设AE=EC=x则有DE=DGEC=AB-EC=3-x,

根据勾股定理得：

x2=（3-x）2+（7）2,解得：

x=2,

•EC=2,

则aec=EC?

AD=■:

2

故选：

D.

【点评】此题考查了旋转的性质，含30度直角三角形的性质，勾股定理，以及等腰三角形

的性质，熟练掌握性质及定理是解本题的关键.

11.（2015?

庆阳）在如图所示的平面直角坐标系中，△OABi是边长为2的等边三角形，作

△B2A2B1与厶OABi关于点Bi成中心对称，再作△B2A3B3与厶B2A2B1关于点B2成中心对称，如此作下去，则△B2nAn+lB2n+1（n是正整数）的顶点An+1的坐标是（）

A.（4n-1,；）B.（2n-1,；）C.（4n+1,；）D.（2n+1,；）

【考点】坐标与图形变化-旋转.

【专题】压轴题；规律型.

【分析】首先根据△OAB1是边长为2的等边三角形，可得A1的坐标为（1，讥j）,B1的坐标为（2,0）;然后根据中心对称的性质，分别求出点怎、A3、A的坐标各是多少；最后总结

出An的坐标的规律，求出A2n+1的坐标是多少即可.

【解答】解：

•••△OAB1是边长为2的等边三角形，

•A1的坐标为（1，品,Bi的坐标为（2,0）,

•/△RAB1与厶OAB1关于点B1成中心对称，

•••点A与点A1关于点_B1成中心对称，

•/2X2-仁3,2X）-：

=-:

•••点A的坐标是（3,-0

•/△E2A3Ba与厶BsAgBi关于点B2成中心对称，

•••点A与点A关于点B2成中心对称，

•••2>4—3=5,2>0-（-7）=7,

•••点A的坐标是（5,近），

•••△&A4B4与厶B3A3B2关于点B3成中心对称，

•点A与点A关于点B成中心对称，

•/2X6-5=7,2>0-二=-7,

•••点A的坐标是（7,-二），

•/1=2X1-1,3=2X2-1,5=2>3-1,7=2X3-1,…，

•An的横坐标是2n-1,A2n+1的横坐标是2（2n+1）-仁4n+1,

•••当n为奇数时，An的纵坐标是当n为偶数时，人的纵坐标是-

•顶点A2n+1的纵坐标是'；,

••△B2nA2n+1B?

n+1（n是正整数）的顶点A2n+1的坐标是（4n+1,~'<）.

故选：

C.

【点评】此题主要考查了坐标与图形变化-旋转问题，要熟练掌握，解答此题的关键是分别

判断出An的横坐标、纵坐标各是多少.

12.（2014?

江西样卷）如图，把图中的△ABC经过一定的变换得到△A'B'C；如果图中△ABC上的点P的坐标为（a,b）,那么它的对应点P的坐标为（）

A.（a-2,b）B.（a+2,b）C.（-a-2,-b）D.（a+2,-b）

【考点】坐标与图形变化-旋转.

【专题】压轴题.

【分析】先根据图形确定出对称中心，然后根据中点公式列式计算即可得解.

【解答】解：

由图可知，△ABC与△ABC关于点（-1,0）成中心对称，设点P的坐标为（x,y）,

所以，—=-1,止=0,

22

解得x=-a-2,y=-b,

所以，P'（-a-2,-b）.

故选C.

【点评】本题考查了坐标与图形变化-旋转，准确识图，观察出两三角形成中心对称，对称

中心是（-1,0）是解题的关键.

13.（2014?

哈尔滨）如图，在Rt△ABC中，/ACB=90,/B=60°,BC=2,△A'B'C可以由△ABC绕点C顺时针旋转得到，其中点A'与点A是对应点，点B与点B是对应点，连接AB',且A

B'、A在同一条直线上，则AA的长为（）

A.6B.47C.37D.3

【考点】旋转的性质.

【专题】几何图形问题.

【分析】利用直角三角形的性质得出AB=4,再利用旋转的性质以及三角形外角的性质得出AB'=2，进而得出答案.

【解答】解：

•••在Rt△ABC中，/ACB=90,/B=60°BC=2

:

丄CAB=30,故AB=4,

•••△A'B'C由厶ABC绕点C顺时针旋转得到，其中点A与点A是对应点，点B与点B是对应点，连接AB；且AB'、A在同一条直线上，

•••AB=AB'=4,AC=AC,

•••/CAA=ZA=30°

•••/ACB=ZBAC=30°,

•AB'=B'C=2,

•AA=2+4=6.

故选：

A.

【点评】此题主要考查了旋转的性质以及直角三角形的性质等知识，得出AB=BC=2是解题

关键.

14.（2015?

贺州）如图，△ODC是由厶OAB绕点O顺时针旋转31°后得到的图形，若点D恰好落在AB上，且/AOC勺度数为100°则/DOB的度数是（）

A.34°B.36°C.38°D.40°

【考点】旋转的性质.

【分析】根据旋转的性质求出/AOD和/BOC的度数，计算出/DOB勺度数.

【解答】解：

由题意得，/AOD=31,/BOC=31,又/AOC=100,

•••/DOB=100-31°-31°38°

故选：

C.

【点评】本题考查的是旋转的性质，掌握旋转角、旋转方向和旋转中心的概念是解题的关键.

15.（2014?

北海）如图，△ABC中，/CAB=65，在同一平面内，将厶ABC绕点A旋转到△AED

的位置，使得DC//AB则/BAE等于（）

F.

A.30°B.40°C.50°D.60°

【考点】旋转的性质.

【专题】计算题.

【分析】先根据平行线的性质得/DCA=/CAB=65,再根据旋转的性质得/BAE=/CADAC=AD则根据等腰三角形的性质得/ADC/DCA=65,然后根据三角形内角和定理计算出

/CAD=180-/ADC-/DCA=50,于是有/BAE=50.

【解答】解：

IDC//AB,

•••/DCA/CAB=65,

•••△ABC绕点A旋转到△AED的位置，

•/BAE=/CADAC=AD

•/ADC/DCA=65,

•/CAD=180-/ADC-/DCA=50,

•/BAE=50.

故选：

C.

【点评】本题考查了旋转的性质：

旋转前后两图形全等；对应点到旋转中心的距离相等；对

应点与旋转中心的连线段的夹角等于旋转角.

二.填空题（共6小题）

16.（2014?

汕头）如图，△ABC绕点A顺时针旋转45°得到△AB'C',若/BAC=90,AB=AC「,则图中阴影部分的面积等于_：

-1.

K■■

【考点】旋转的性质；等腰直角三角形.

【专题】压轴题.

【分析】根据题意结合旋转的性质以及等腰直角三角形的性质得出AD=,BC=1,

t—i

AF=FC=sin45°AC=AC=1，进而求出阴影部分的面积.

【解答】解：

•••△ABC绕点A顺时针旋转45°得到△A'B'C',/BAC=90,AB=AC=,

•••BC=2,/C=ZB=ZCAC=ZC'=45°

•••AD丄BC,B'C'丄AB,

•AD=BC=1,AF=FC=sin45°AC=JAC=1,

22

•图中阴影部分的面积等于：

S^AFC—SaDE

22

故答案为：

1.

c

B

即可得出/解：

•••把△ABC绕点C按顺时针方向旋转35°得到△A'B'C,

A的度数.

AB交AC于点D,

A的度数是解题

【点评】此题主要考查了旋转的性质以及等腰直角三角形的性质等知识，得出AD,AF,DC

的长是解题关键.

17.（2014?

梅州）如图，把△ABC绕点C按顺时针方向旋转35°得到△A'B'C,AB交AC于

【解答】

/A'DC=90,

•••/ACA=35°则/A=90°-35°=55°,

则/A=ZA'=55°

故答案为：

55°.

【点评】此题主要考查了旋转的性质以及三角形内角和定理等知识，得出/关键.

18.（2014?

绵阳）如图，在正方形ABCD中,E、F分别是边BCCD上的点，/EAF=45°,△ECF的周长为4,则正方形ABCD勺边长为2.

【考点】旋转的性质；全等三角形的判定与性质；勾股定理；正方形的性质.

【专题】计算题.

【分析】根据旋转的性质得出/EAF=45°进而得出△FAE^AEAF；即可得出

EF+EC+FC=FC+CE+EFC+BC+B丘4，得出正方形边长即可.

【解答】解：

将ADAF绕点A顺时针旋转90度到ABAF位置，由题意可得出：

△DAF^ABAF,

•••DF=BF,/DAF玄BAF',

•••/EAF=45°

在厶FAE和厶EAF中

fAF=AFy

弋ZFAE-ZEAFy,

二AE

•△FAE^AEAF（SAS,

•EF=EF,

•••△ECF的周长为4,

•EF+EC+FC=FC+CE+EFC+BC+BF：

DF+FC+BC=,

•2BC=4,

•BC=2.

【点评】此题主要考查了旋转的性质以及全等三角形的判定与性质等知识，得出

△FAE^AEAF是解题关键.

19.（2014?

白银）如图，四边形ABCD是菱形，O是两条对角线的交点，过0点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为6和8时，则阴影部分的面积

【考点】中心对称；菱形的性质.

【专题】几何图形问题.

【分析】根据菱形的面积等于对角线乘积的一半求出面积，再根据中心对称的性质判断出阴

影部分的面积等于菱形的面积的一半解答.

【解答】解：

•••菱形的两条对角线的长分别为6和8,

•••菱形的面积=->6>8=24,

2

•/O是菱形两条对角线的交点，

•••阴影部分的面积=「>4=12.

2

故答案为：

12.

【点评】本题考查了中心对称，菱形的性质，熟记性质并判断出阴影部分的面积等于菱形的面积的一半是解题的关键.

20.（2014?

陕西）如图，在正方形ABCD中,AD=1,将厶ABD绕点B顺时针旋转45°得到△A'BD,此时A'D'与CD交于点E，贝UDE的长度为2-匚.

【考点】旋转的性质.

【专题】几何图形问题.

【分析】利用正方形和旋转的性质得出AD=AE，进而利用勾股定理得出BD的长，进而利用

锐角三角函数关系得出DE的长即可.

【解答】解：

由题意可得出：

/BDC=45，/DAE=90°，

•••/DEA=45°

•A'D=AE，

•••在正方形ABCD中,AD=1，

•AB=AB=1，

•BD=］，

•A'D=1，

•••在Rt△DAE中，

DE=2=2-匚.

sin45

故答案为：

2-匚.

【点评】此题主要考查了正方形和旋转的性质以及勾股定理、锐角三角函数关系等知识，得

出A'D的长是解题关键.

21.（2014?

黑龙江）如图，等腰Rt△ABC中，/ACB=9C°AC=BC=1且AC边在直线a上,将厶ABC绕点A顺时针旋转到位置①可得到点R,此时AF1^2；将位置①的三角形绕点

R顺时针旋转到位置②，可得到点P2,此时AR=1+匚；将位置②的三角形绕点P2顺时针

旋转到位置③，可得到点P3,此时AR=2+匚；…，按此规律继续旋转，直至得到点P2014为

止.贝yAF2oi4=1342+672二

【考点】旋转的性质.

【专题】规律型.

【分析】由已知得AR=J^,AP2=1+逅,AP3=2+^2；再根据图形可得到AR=2+2、应；AP=3+2-/^;AR=4+2匚;AF7=4+3匚；AF8=5+3匚；AF9=6+3匚；每三个一组，由于2013=3071,贝UARoi3=

（2013-671）+671二，然后把AF2oi3加上-即可.

【解答】解：

AR=匚，AF2=1+匚,AF3=2+匚；

AR=2+2二；AF5=3+2*j；AF6=4+2二；

AF7=4+3二；AF8=5+3“J:

「；AF9=6+3二；

•/2013=3>671,

二AP2013=（2013-671）+671「=1342+671二,

•••AF2014=1342+671匚+==1342+672匚.

故答案为：

1342+672唧-.

【点评】本题考查了旋转的性质：

旋转前后两图形全等；对应点到旋转中心的距离相等；对

应点与旋转中心的连线段的夹角等于旋转角.

三.解答题（共8小题）

22.（2014?

咸宁）如图，在