数学运算 秒杀技巧培训资料.docx

数学运算 秒杀技巧培训资料.docx

《数学运算 秒杀技巧培训资料.docx》由会员分享，可在线阅读，更多相关《数学运算 秒杀技巧培训资料.docx（30页珍藏版）》请在冰豆网上搜索。

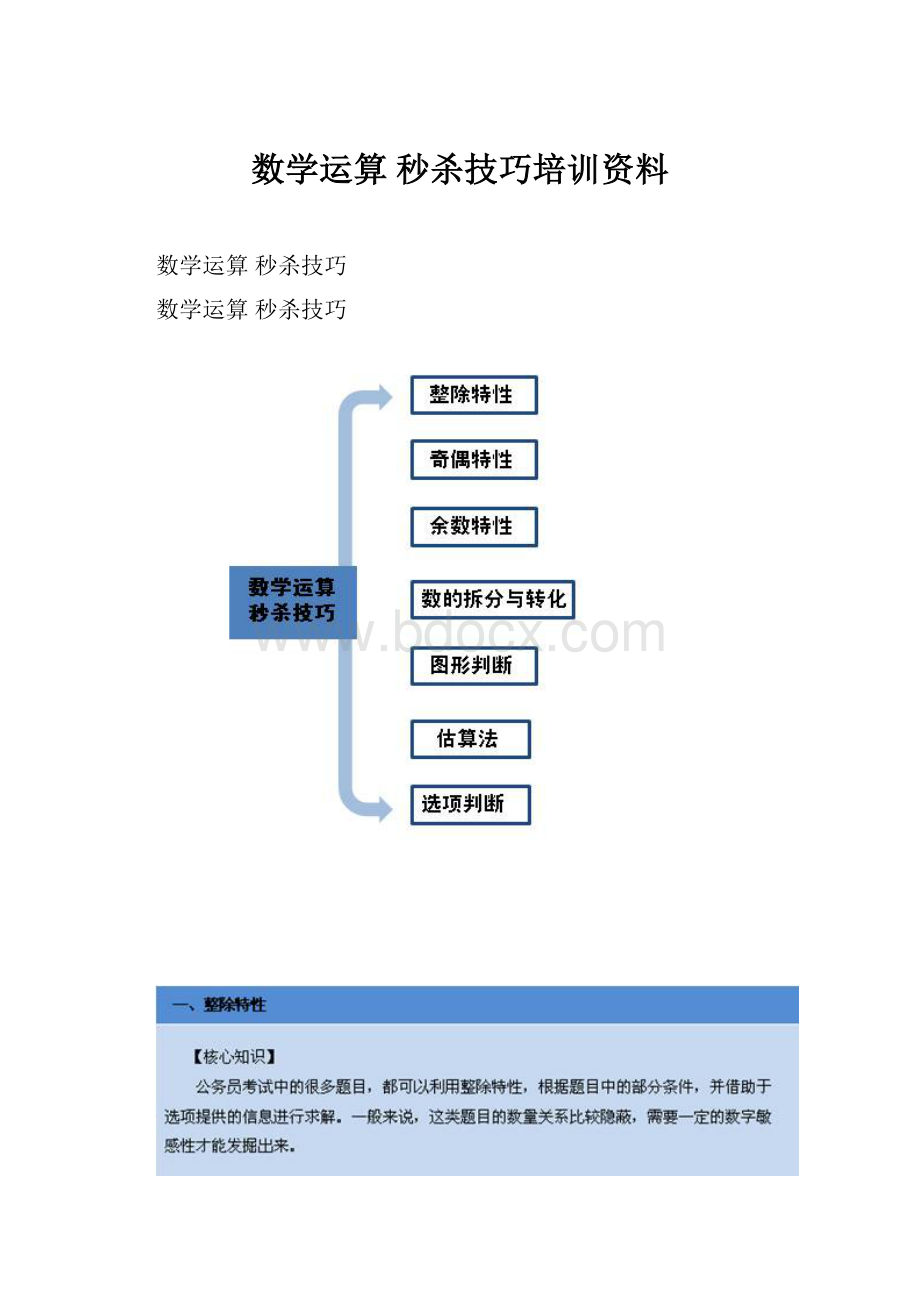
数学运算秒杀技巧培训资料

数学运算秒杀技巧

数学运算秒杀技巧

  【真题精析】

   例1:

（2009．河南）1×2×3+2×3X4+3×4×5+…+28×29×30=（    ）

    A.188690    B.188790    C.188890    D.188990

   [答案]B

   [秒杀]每一项都是三个连续自然数的乘积，则结果一定能被3整除。

分析选项，只有B符合。

【真题精析】

  例l：

（2004．山东）某次测验有50道判断题，每做对一题得3分，不做或做错一题倒扣1分，某学生共得82分，问答对题数和答错题数（包括不做）相差多少？

    A．33    B 39    C．17    D．16

 [答案]D

 [秒杀]根据题意，答对的题目数十答错的题目数一总题目数50（偶数），故二者之差也应是偶数。

分析选项，只有D符合。

 [解析]设答对题数为x，答错题数（包括不做）为y，则有

，

所以答对题数和答错题数（包括不做）相差为16。

【真题精析】

例1：

（2006．国考）一个三位数除以9余7，除以5余2，除以4余3，这样的三位数共有：

A．5个    B．6个    C．7个    D．8个

 [答案]A

 [秒杀]周期为4，5，9的最小公倍数9×5×4=180。

由于1000÷180=5------100，而满足条件的最小三位数一定大于100，故共有5个数字。

    [解析]运用中国剩余定理，计算出最小的符合题意的数字为187，而4，5，6的最小公倍数为180，则

187+180n<1000，有5个数字。

【真题精析】

     例1：

（2005．湖南）一堆沙重480吨，用5辆载重相同的汽车运3次，完成了运输任务的25%，余下的沙由9辆同样的汽车来运，几次可以运完？

    A．4次    B．5次    C．6次    D．7次

 [答案]B

 [秒杀]根据“用5辆载重相同的汽车运3次，完成了运输任务的25%”可知，剩下的1-25%=75%可由这5辆载重相同的汽车运9次，即相当于9辆相同的汽车运5次。

因此，选B。

 [解析]5辆汽车3次运沙480×25%=120吨，即每辆车每次可以运沙8吨。

故9辆车每次可以运沙72吨，则剩下的360吨需要运输360÷72=5次。

【真题精析】

  例1：

（2008．江西）A、B、C、D、E这5个小组开展扑克比赛，每两个小组之间都

要比赛一场，到现在为止，A组已经比赛了4场，B组已经比赛3场，C组已经比赛了

2场，D组已经比赛了1场。

问E组比了几场？

                              A．0    B．1

                              C．2    D．3

 [答案]C

  [秒杀]将五位人的比赛关系用右图表示，因此，选C。

  [解析]显然A组与B、C、D、E都比赛了一场，则D组只能和A组比赛了一场，B组只能和A、C、E各比赛一场，C组只能和A、B各比赛一场，因此D组只和A、B各比赛一场，答案为C。

【真题精析】

  例1:

（873×477-198）÷（476×874+199）=（    ）

  A．1    B．2    C．3    D．4

  [答案]A

  [秒杀]873×477-198与476×874+199数值相差不大，故二者之商一定小于2。

因此，选A。

  [解析]原式=

   【真题精析】

    例1：

有甲、乙两个项目组，乙组任务临时加重时，从甲组抽调了四分之一的组员。

此后甲组任务也有所加重，于是又从乙组调回了重组后乙组人数的十分之一。

此时甲组与乙组人数相等。

由此可以得出结论：

    A.甲组原有16人，乙组原有11人    B．甲、乙两组原组员人数之比为16：

11

    C．甲组原有11人，乙组原有16人    D．甲、乙两组原组员人数比为11：

16

    [答案]B

    [秒杀]分析选项，B、D包含了A、C的情况，即如果B.D正确，则A、C正确，故可以排除A、C。

根据“乙组任务临时加重时，从甲组抽调了四分之一的组员。

此后甲组任务也有所加重，于是又从乙组调回了重组后乙组人数的十分之一。

此时甲组与乙组人数相等”可以判断出甲组人数多于乙组，排除D0因此，选B。

[解析]根据题意：

设甲组原有x人，乙组原有y人，则有，

解得        。

因此，选B。

数学运算常用解题思路

第一节    技巧性方法

【真题精析】

例1.（2008．广东）某人工作一年的报酬是18000元和一台全自动洗衣机．他干了7个月，得到9500元和一台全自动洗衣机，问这台洗衣机值多少元？

    A．8500元    B．2400元    C．2000元    D．1700元

[答案]B

[秒杀技巧]解题关键是每个月所得报酬相同。

[解析]设这台洗衣机值x元，则                       ，解得x=2400。

【真题精析】

例1.（2006．江苏B类）某体育训练中心，教练员中男占90%，运动员中男占80%，在教练员和运动员中男占82%，教练员与运动员人数之比是：

    A．2:

5    B．1:

3    C．1:

4    D．1:

5

[答案]C

[解析]运用十字交叉法有：

所以男教练员与男运动员人数之比为2%：

8%=1：

4。

【真题精析】

例1.（2007．安徽）一个最简分数，分子和分母的和是50，如果分子、分母都减去5，得到的最简分数是2/3，这个分数原来是多少？

  A．20/29    B．21/29    C．29/30    D．29/50

[答案]B

[解析]根据“分子和分母的和是50”，只有B项正确。

【真题精析】

例1.（2007．江西）设

    A．10/9    B．11/9    C．7/9    D．5/7

[答案]B

[解析]根据

第二节  思路性方法

【真题精析】

例1.（2007．西藏）一种挥发性药水，原来有一整瓶，第二天挥发后变为原来的1/2；第三天变为第二天的2/3；第四天变为第三天的3/4，请问第几天时药水还剩下1/30瓶？

    A．5天    B．12天    C．30天    D．100天

[答案]C

[解析]根据题意可知，第二天剩下的药水为整瓶的1/2，第三天剩下的药水为整瓶的1/2×2/3=1/3，第四天剩下的药水为整瓶的1/3×3/4=1/4，以此类推，第30天剩下的药水为整瓶的1/30。

【真题精析】

例1.（2008．吉林甲级）有个人发现图书馆的那本《大英百科全书》的第21、42、64、65、121、137、138、190页对他有用，便把这几页偷偷的撕下带走了，那他一共撕去了：

    A．4张    B．6张    C．7张    D．8张

[答案]C

[秒杀技巧]不连续的数字肯定不能占据一张纸，连续数字存在占据同一张纸上的可能。

[解析]由题意可知，在所给出的页码中，有两组连续的页码，即64、65和137、138。

假设64和65是同一张纸，则137和138页必不在同一张纸上；反之亦然。

因此，他只可能撕去7张纸。

【真题精析】

例1.2007．浙江）某部队战士排成了一个6行、8列的长方阵。

现在要求各行从左至右1，2，1，2，1，2，1，2报数，再各列从前到后1，2，3，1，2，3报数。

问在两次报数中，所报数字不同的战士有：

    A．18个    B．24个    C．32个    D．36个

[答案]C

[解析]根据题意可列表如下：

  表格中用“★”标记的即为每次报数相同的战士，故每列中两次所报数字不同的战士数均为4，故共有4×8=32个战士两次所报数字不同。

因此，选C。

容斥原理问题——基础学习

一、解答题

2、两个集合容斥原理例1：

四年级一班有54人，定阅《小学生优秀作文》和《数学大世界》两种读物的有13人，订阅《小学生优秀作文》的有45人每人至少订阅一种读物，订阅《数学大世界》的有多少人？

（    ）

A．13           B．22        C．33          D．41

【答案】B

【解题关键点】设A={定阅《小学生优秀作文》的人}，B={订阅《数学大世界》的人}，那么A∩B={同时订阅两本读物的人}，A∪B={至少订阅一样的人}，由容斥原则，B=A∪B+A∩B-A=54+13-45=22人。

【结束】

3、两个集合容斥原理例2：

五年级有122名同学参加语文、数学考试，每个至少有一门功课取得优秀成绩，其中语文成绩优秀的有65人，数学成绩优秀的有87人。

语文、数学都优秀的有多少人？

（　）

A． 30      B．35        C．57          D．65

【答案】A

【解题关键点】此题是典型的两个集合的容斥问题，因此，可以直接有两个集合的容斥原理得到，语文和数学都优秀的学生有65+87-122=30人。

【结束】

4、两个集合容斥原理例3：

学校文艺组每人至少会演奏一种乐器，已知会拉手提琴的有24人，会弹电子琴的有17人，其中两样都会的有8人。

这个文艺组共有多少人？

（  ）

A．25           B．32        C．33          D．41

【答案】C

【解题关键点】设A={会拉手提琴的}，B={会弹电子琴的}，因此A∪B={文艺组的人}，A∩B={两样都会的}，由两个集合的容斥原理可得：

A∪B=A+B-A∩B=24+17-8=33。

【结束】

5、两个集合容斥原理例4：

某班有36个同学在一项测试中，答对第一题的有25人，答对第二题的人有23人，两题都答对的有15人，问多少个同学两道题都没有答对？

（   ）

A．1            B．2         C．3           D．4

【答案】C

【解题关键点】有两个集合的容斥原理得到，至少答对一道题的同学有25+23-15=33人，因此两道题都没有答对的同学有36-33=3人。

【结束】

7、三个集合容斥原理例1：

某大学有外语教师120名，其中教英语的有50名，教日语的有45名，教法语的有40名，有15名既教英语又教日语，有10名既教英语又教法语，有8名既日语又教法语，有4名教英语、日语和法语三门课，则不交三门课的外语教师有多少名？

（    ）

A．12           B．14        C．16          D．18

【答案】B

【解题关键点】此题是三个集合的容斥问题，根据容斥原理可以得到，至少教英、日、法三门课其中一门的外语教师有50+45+40-10-8-4=106，不做这三门课的外语教师人数为120-106=14名。

【结束】

8、三个集合容斥原理例2：

对厦门大学计算机系100名学生进行调查，结果发现他们喜欢看NBA和足球、赛车。

其中58人喜欢看NBA；38人喜欢看赛车，52人喜欢看足球，既喜欢看NBA又喜欢看赛车的有18人，既喜欢看足球又喜欢看赛车的有16人，三种都喜欢看的有12人，则只喜欢看足球的有（ ）。

A．22人         B．  28人        C．30人            D．36人

【答案】A

【解题关键点】求只喜欢看足球的，只要种人数减去喜欢看NBA和喜欢看赛车的，但多减去了既喜欢看NBA又喜欢看赛车的，再加回去即可，100-58-38+18=22人。

【结束】

9、三个集合容斥原理例3：

实验小学举办学术书法展，学校的橱窗里展出了每个年级学生的书法作品，其中有28幅不是五年级的，有24幅不是六年级的，五、六年级参展作品共有20幅。

一、二年级参展的作品总数比三、四年级参展的作品总数少4幅。

一、二年级参展的书法作品共有多少幅？

（    ）

A．6            B．10        C．16          D．20

【答案】A

【解题关键点】28幅不是五年级的，也就是六年级+其他年级=28幅；24幅不是六年级的，也就是五年级+其他年级=24幅；上述两个式子相加得，（五年级+六年级）+2×其他年级=28+24，因此其他年级的有（28+24-20）÷2=16幅，又因为一、二年级参展的作品总数比三、四年级参展的作品总数少4幅，因此一、二年级参展的书法作品共有（16-2）÷2=6幅。

【结束】

10、三个集合容斥原理例4：

某工作组有12名外国人，其中6人会说英语，5人会说法语，5人会说西班牙语;有3人既会说英语又会说法语，有2人既会说法语又会说西班牙语，有2人既会说西班牙语又会说英语;有1人这三种语言都会说。

则只会说一种语言的人比一种语言都不会说的人多（）。

A.1人      B.2人      C.3人      D.5人

【答案】C。

【解题关键点】如图所示：

上图的含义为只懂英语、法语和西班牙语的人数分别人2、1和2，共5人，而一种语言都不会说的人数为12-（2+2+1+1+1+1+2）=2（人），5-2=3（人）。

【结束】

浓度问题——基础学习

一、     解答题

3、求混合之前的初始状态例1：

现有一种预防甲型H1N1流感的药物配制成的甲、乙两种浓度不同的消毒液。

若从甲中取2100克，乙中取700克混合而成的消毒溶液的浓度为3%，若从甲中取900克，乙中取2700克，则混合而成的消毒溶液的浓度为5%，则甲、乙两种消毒溶液的浓度分别为（   ）。

    A．3%，6%           B．3%，4%        C．2%，6%  D．4%，6%

【答案】C

【解题关键点】设甲、乙两种溶液溶液浓度分别是x，y，则2100x+700y=（2100+700）×3%，900x+2700y=（900+2700）×5%，解得x=2%，y=6%。

【结束】

4、求混合之前的初始状态例2：

取甲种硫酸300克和乙种硫酸250克，再加水200克，可混合成浓度为50%的硫酸；而取甲种硫酸200克和乙种硫酸150克，再加上纯硫酸200克，克混合成浓度为80%的硫酸。

那么甲、乙两种硫酸的浓度各是多少？

（      ）

    A．75%，60%     B．68%，63%    C．71%，73% D．59%，65%

【答案】A

【解题关键点】设甲、乙硫酸浓度分别是x、y，则300x+250y=（300+250+200）×50%，200x+150y+200=（200+150+200）×80%，解得x=75%，y=60%。

【结束】

6、求混合后的最终状态例1：

130克含盐5%的盐水，含盐9%的盐水混合，配成含盐6.4%的盐水，这样配成的6.4%的盐水有多少克（      ）

    A．120          B．180       C．200     D．300

【答案】C

【解题关键点】设配成的盐水有x克，则可列方程130×5%+（x-130）×9%=x×6.4%，解得x=200。

【结束】

8、增加溶剂（稀释问题）例1：

有浓度为60%的溶液若干，加了一定数量的水后，稀释成48%的溶液，如果再加入同样多的水，浓度是多少？

（        ）

    A．40%          B．45%       C．50% D．55%

【答案】A

【解题关键点】设原有溶液a克，加入水x克，最后浓度为y，60%a=48%（a+x）=y（a+2x）。

解得y=40%。

【结束】

10、减少溶剂（蒸发问题）例1：

13000千克青菜，早晨测得它的含水率为97%，这些菜到了下午测得含水率为95%，那么这些菜的重量减少了（      ）千克。

    A． 200     B．300       C．400      D．500

【答案】C

【解题关键点】青菜中除了水之外的其他成分质量不会变化，下午含水率为95%的菜重量为1000×（1—97%）÷（1-95%）=600千克，所以青菜重量减少了1000-600=400千克，选择C。

【结束】

11、减少溶剂（蒸发问题）例2：

有浓度为4%的盐水若干千克，蒸发了一些水分后浓度变成10%，再加入300克40%的盐水后，浓度变为6.4%的盐水，问最初的盐水多少克？

（        ）

    A． 200     B．300       C．400      D．500

【答案】D

【解题关键点】首先，根据题意，可以用十字交叉法确定与300克4%的盐水混合得到浓度为6.4%盐水的10%浓度盐水的重量为200克。

再设最初盐水x克，则200×10%=x×4%，可得x=500克。

【结束】

12、推导法（按题意从初始状态逐步计算直至最终状态）例1：

一满杯水溶有10克糖，搅匀后喝去

；添入6克糖，加满水搅匀，再喝去

；添入6克糖，再加满水搅匀，又喝去

；再添入6克糖，加满水搅匀，仍喝去

。

问：

此时杯中所剩的糖水中有多少克糖？

（      ）

    A.

     B.

      C.

    D.5

【答案】A

【解题关键点】初始杯中含有10克糖，喝完第一次后剩

×10克糖，喝完第二次剩（

）

×10克糖，喝完第三次剩（

）

×10克糖，喝完第四次剩（

）

×10=

克。

第二次加入的6克糖，喝完第一次后剩

×6克糖，喝完第三次剩（

）

×6克糖，喝完第四次后剩（

）

×6=

克糖，第三次加入的6克糖，喝完第三次后还剩

×6克糖，喝完第四次后剩（

）

×6=

克糖。

第四次加入的6克糖，当喝完第四次后还剩

×6=2克糖。

综上分析，最后杯中含糖

+

+

+2=3

克糖。

【结束】

13、推导法（从最终状态逆推求出初始状态）例1：

有浓度为4%的盐水若干千克，蒸发了一些水分后浓度变成10%，再加入300克40%的盐水后，浓度变为6.4%的盐水，问最初的盐水多少克？

（      ）

    A． 200     B．300       C．400      D．500

【答案】D

【解题关键点】首先，根据题意，可以用十字交叉法确定与300克4%的盐水混合得到浓度为6.4%盐水的10%浓度盐水的重量为200克。

再设最初盐水x克，则200×10%=x×4%，可得x=500克。

【结束】

15、方程法例1：

甲、乙两杯奶茶分别重300克和120克，甲中含奶茶粉120克，乙中含奶茶粉90克。

从两杯中应各取出多少克才能兑成浓度为50%的奶茶140克？

（       ）

    A． 90，50      B．100，40       C．110，30      D．120，20

【答案】B

【解题关键点】可设取出甲x克，乙（140-x）克，那么，[x×

+

×（140-x）] ÷140=50%，解得x=100.所以取100克的甲，取140-100=40克的乙。

【结束】

16、方程法例2：

130克含盐5%的盐水，与含盐9%的盐水混合，配成含盐6.4%的盐水，这样配成的6.4%的盐水有多少克（      ）

    A．120          B．180       C．200      D．300

【答案】C

【解题关键点】设配成的盐水有x克，则克列方程130×5%+（x-130）×9%=x×6.4%，解得x=200.

【结束】

18、十字交叉法例1：

在浓度为75%的酒精中加入10千克水，浓度变为35%，再加入L千克纯酒精，浓度变为60%，则L为多少千克？

（      ）

    A．8            B．11.7     C．14.6     D．16.4

【答案】B

【解题关键点】十字交叉法。

第一次混合相当于浓度为75%与0%的溶液混合。

75%的酒精   75%    35%

       ＼∕

        35% 

       ∕＼

水         0%    40%

所以75%的酒精与水的比例为35：

40=7：

8。

水10千克，75%的酒精8.75千克，混合后共18.7千克。

第二次混合，相当于浓度为35%与100%的溶液混合。

35%的酒精  35%    40%

    ＼∕

     60% 

    ∕＼

纯酒精     100%   25%

所以35%的酒精与纯酒精的比例为40：

25=8：

5，即18.75：

L=8：

5，L≈11.7千克。

【结束】

19、十字交叉法例2：

把浓度为20%、40%和60%的某溶液混合在一起，得到浓度为36%的溶液50升。

已知浓度为40%的溶液用量是浓度为20%的溶液用量的3倍。

浓度为40%的溶液的用量是多少升？

（       ）

    A． 36      B．38        C．44     D．46

【答案】A

【解题关键点】设20%的溶液为x升，则40%的溶液为3x升，相当于（20%×x+40%×3x）÷4x=35%的溶液4x升与60%的溶液y升混合。

用十字交叉法，则

所以4x：

y=24：

1，即x=6y。

带入方程35%×4x+60y=36%×50，解得x=12，所以浓度为40%的溶液用了3x=36升。

【结束】

20、分析猜答案法：

深刻理解混合的本质（公式的理解），分析题目才出答案；

21、分析猜答案法例1：

现有一种预防禽流感药物配置成的甲、乙两种不同浓度的消毒溶液，若从甲中取2100克，乙中取700克混合而成的消毒溶液的浓度为3%；若甲种取900克，乙中取2700克，则混合而成的消毒溶液的浓度为5%，则甲、乙两种消毒溶液的浓度分别为（   ）

A.3%，6%      B.3%,4%      C.2%,6%       D.4%,6%

【答案】C

【解题关键点】首先可以根据溶质相等，构造方程。

      方程法：

设甲、乙溶液的浓度分别为x、y，则

通过解方程可以得到答案，但是此种方法会用掉比较多的时间，所以我们应该寻找更为简便的做法。

       分析猜提法：

题目中说一定量的甲溶液和一定量的乙溶液混合，得到3%溶液，则可以说明，甲、乙溶液浓度一种大于3%，一种小于3%。

同理可得，甲、乙溶液浓度一种大于5%，另一种小于5%，综合得出甲、乙溶液一种大于5%，一种小于3%从选项可以看出，答案为C.

【结束】