七年级数学下册143整式的乘法教案学案练习.docx

七年级数学下册143整式的乘法教案学案练习.docx

《七年级数学下册143整式的乘法教案学案练习.docx》由会员分享，可在线阅读，更多相关《七年级数学下册143整式的乘法教案学案练习.docx（10页珍藏版）》请在冰豆网上搜索。

七年级数学下册143整式的乘法教案学案练习

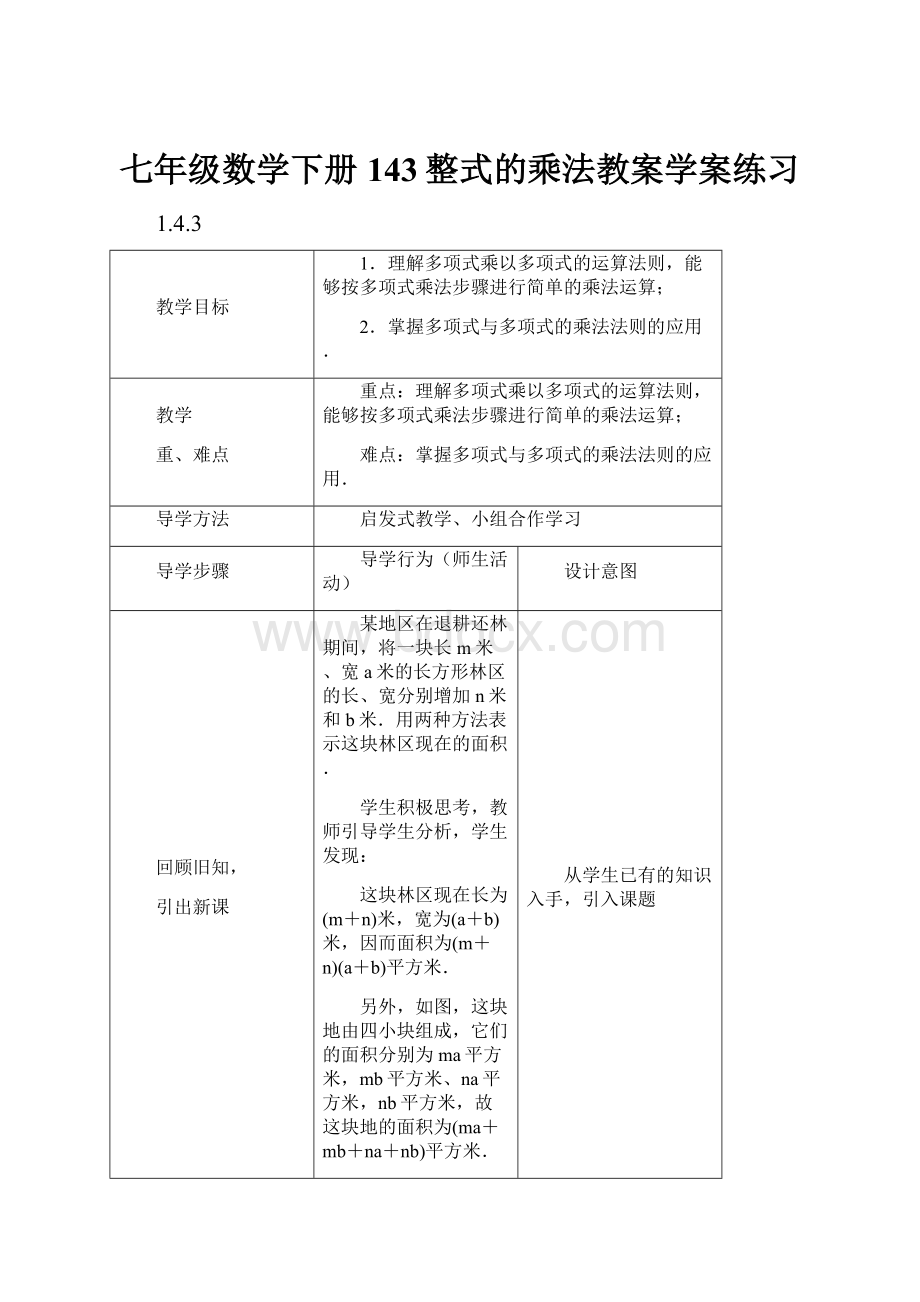
1.4.3

教学目标

1．理解多项式乘以多项式的运算法则，能够按多项式乘法步骤进行简单的乘法运算；

2．掌握多项式与多项式的乘法法则的应用．

教学

重、难点

重点：

理解多项式乘以多项式的运算法则，能够按多项式乘法步骤进行简单的乘法运算；

难点：

掌握多项式与多项式的乘法法则的应用．

导学方法

启发式教学、小组合作学习

导学步骤

导学行为（师生活动）

设计意图

回顾旧知，

引出新课

某地区在退耕还林期间，将一块长m米、宽a米的长方形林区的长、宽分别增加n米和b米．用两种方法表示这块林区现在的面积．

学生积极思考，教师引导学生分析，学生发现：

这块林区现在长为（m＋n）米，宽为（a＋b）米，因而面积为（m＋n）（a＋b）平方米．

另外，如图，这块地由四小块组成，它们的面积分别为ma平方米，mb平方米、na平方米，nb平方米，故这块地的面积为（ma＋mb＋na＋nb）平方米．

由此可得（m＋n）（a＋b）＝ma＋mb＋na＋nb.今天我们就学习多项式乘以多项式．

从学生已有的知识入手，引入课题

新知探索

例题

精讲

合作探究

探究点一：

多项式与多项式相乘

【类型一】直接利用多项式乘多项式法则进行计算

计算：

（1）（3x＋2）（x＋2）；

（2）（4y－1）（5－y）．

解析：

利用多项式乘以多项式法则计算，即可得到结果．

解：

（1）原式＝3x2＋6x＋2x＋4＝3x2＋8x＋4；

（2）原式＝20y－4y2－5＋y＝－4y2＋21y－5.

方法总结：

多项式乘以多项式，按一定的顺序进行，必须做到不重不漏；多项式与多项式相乘，仍得多项式，在合并同类项之前，积的项数应等于原多项式的项数之积．

【类型二】多项式乘以多项式的混合运算

计算：

（3a＋1）（2a－3）－（6a－5）（a－4）．

解析：

根据整式混合运算的顺序和法则分别进行计算，再把所得结果合并即可．

解：

（3a＋1）（2a－3）－（6a－5）（a－4）＝6a2－9a＋2a－3－6a2＋24a＋5a－20＝22a－23.

方法总结：

在计算时要注意混合运算的顺序和法则以及运算结果的符号．

探究点二：

多项式与多项式相乘的化简求值及应用

【类型一】多项式乘以多项式的化简求值

先化简，再求值：

（a－2b）（a2＋2ab＋4b2）－a（a－5b）（a＋3b），其中a＝－1，b＝1.

解析：

先将式子利用整式乘法展开，合并同类项化简，再代入计算．

解：

（a－2b）（a2＋2ab＋4b2）－a（a－5b）（a＋3b）＝a3－8b3－（a2－5ab）（a＋3b）＝a3－8b3－a3－3a2b＋5a2b＋15ab2＝－8b3＋2a2b＋15ab2.当a＝－1，b＝1时，原式＝－8＋2－15＝－21.

方法总结：

化简求值是整式运算中常见的题型，一定要注意先化简，再求值，不能先代值，再计算．

【类型二】多项式乘以多项式与方程的综合

解方程：

（x－3）（x－2）＝（x＋9）（x＋1）＋4.

解析：

方程两边利用多项式乘以多项式法则计算，移项、合并同类项，将x系数化为1，即可求出解．

解：

去括号后得x2－5x＋6＝x2＋10x＋9＋4，移项、合并同类项得－15x＝7，解得x＝－

.

方法总结：

解答本题就是利用多项式的乘法，将原方程转化为已学过的方程解答．

【类型三】多项式乘以多项式的实际应用

千年古镇杨家滩的某小区的内坝是一块长为（3a＋b）米，宽为（2a＋b）米的长方形地块，物业部门计划将内坝进行绿化（如图阴影部分），中间部分将修建一仿古小景点（如图中间的正方形），则绿化的面积是多少平方米？

并求出当a＝3，b＝2时的绿化面积．

解析：

根据长方形的面积公式，可得内坝、景点的面积，根据面积的差，可得答案．

解：

由题意，得（3a＋b）（2a＋b）－（a＋b）2＝6a2＋5ab＋b2－a2－2ab－b2＝5a2＋3ab（平方米）．当a＝3，b＝2时，5a2＋3ab＝5×32＋3×3×2＝63（平方米），故绿化的面积是63平方米．

方法总结：

掌握长方形的面积公式和多项式乘多项式法则是解题的关键．

【类型四】根据多项式乘以多项式求待定系数的值

已知ax2＋bx＋1（a≠0）与3x－2的积不含x2项，也不含x项，求系数a、b的值．

解析：

首先利用多项式乘法法则计算出（ax2＋bx＋1）（3x－2），再根据积不含x2项，也不含x项，可得含x2项和含x项的系数等于零，即可求出a与b的值．

解：

（ax2＋bx＋1）（3x－2）＝3ax3－2ax2＋3bx2－2bx＋3x－2.∵积不含x2项，也不含x项，∴－2a＋3b＝0，－2b＋3＝0，解得b＝

，a＝

，∴系数a、b的值分别是

，

.

方法总结：

解决此类问题首先要利用多项式乘法法则计算出展开式，合并同类项后，再根据不含某一项，可得这一项系数等于零，再列出方程解答．

引出研究本节课要学习知识的必要性，清楚新知识的引出是由于实际生活的需要

学生积极参与学习活动，为学生动脑思考提供机会，发挥学生的想象力和创造性

体现教师的主导作用

学以致用，

举一反三

教师给出准确概念，同时给学生消化、吸收时间，当堂掌握

例2由学生口答，教师板书，

课堂检测

1.关于x的一次二项式的积（x-3）（x+a）中常数项为21，则a的值是（）

A.7B.-7C.4D.-4

2．长方形相邻的两边长分别为2a-b与a+2b，那么这个长方形的面积是（）

A.2a2-3ab-2b2　B.2a2+3ab-2b2

C.2a2+5ab+2b2　　D.2a2-5ab-2b2

3．下列各式中，错误的是（）

A.（x+2）（x-3）＝x2-x-6

B.（x－4）（x＋4）＝x2-16

C.（2x+3）（2x-6）＝2x2-3x-18　

D.（2x－1）（2x＋2）＝4x2＋2x-2

4．如果（x-5）（x+6）＝x2+mx+n，那么m、n的值分别为（）

A.1，－30B.－1，30

C.－1，－30　D.1，30

5．计算：

（x-2）（x+1）＝＿＿＿＿＿＿＿＿＿；

（a+b）（a-b）＝＿＿＿＿＿＿＿＿＿；

（2a+3）（4a-5）＝＿＿＿＿＿＿＿＿＿＿＿．

6．先化简，再求值：

（2x-1）2＋（x+2）（x-2）－4x（x-1），其中x=3．

7．如图，梯形的上底长为3x，下底长为5x-y，高为3x+2y，求这个梯形的面积．

8.已知x2-5x=14，求（x-1）（2x-1）-（x+1）2+1的值.

检验学生学习效果，学生独立完成相应的练习，教师批阅部分学生，让优秀生帮助批阅并为学困生讲解.

总结提升

总结本节课的主要内容：

1．多项式与多项式的乘法法则：

多项式和多项式相乘，先用一个多项式的每一项与另一个多项式的每一项相乘，再把所得的积相加．

2．多项式与多项式乘法的应用

板书设计

1.4.3整式的乘法

（一）知识回顾（三）例题解析（五）课堂小结

（二）探索新知例1、例2

（四）课堂练习练习设计

本课作业

教材P19随堂练习

本课教育评注（实际教学效果及改进设想）

1.4.3整式的乘法

一、预习与质疑（课前学习区）

（一）预习内容：

P18-P19

（二）预习时间：

10分钟

（三）预习目标：

1．理解多项式乘以多项式的运算法则，能够按多项式乘法步骤进行简单的乘法运算；

2．掌握多项式与多项式的乘法法则的应用．

（四）学习建议：

1．教学重点：

理解多项式乘以多项式的运算法则，能够按多项式乘法步骤进行简单的乘法运算；

2．教学难点：

掌握多项式与多项式的乘法法则的应用．

（五）预习检测：

1.单项式与多项式相乘，用单项式乘多项式的每一项，再把所得的相加，即a（b+c+d）=ab+ac+ad。

2.计算

（1）（-3x2）·（4x-3）

（2）（-2a2）（3ab2-5ab3）；

（3）（a+4）（a+3）

（4）（2x－5y）（3x－y）

（5）n（n+1）（n+2）

（6）

活动一：

合作探究：

1、计算：

（1）（1－x）（0.6－x）

（2）（2x＋y）（x－y）

（3）（－2m－1）（3m－2）（4）

2、先化简,再求值:

（2x－1）（4x2＋2x＋1），其中

3、解方程:

（3x+2）（x－1）=3（x－1）（x+1）.

（六）生成问题：

通过预习和做检测题你还有哪些疑惑请写在下面。

二、落实与整合（课中学习区）

活动二：

精讲点拨：

（1）多项式乘多项式的运算法则；

（2）多项式乘多项式是如何转化为单项式的.

（3）（a+n）（m+b）＝a（m+b）+n（m+b）＝am+ab+mn+bn

用文字表示为__________________________

计算：

（1）

；

（2）

.

交流展示：

（1）（x+y）（x-y）=（）；

（2）（x-y）2＝（）；

（3）（a+b）（x+y）＝（）；（4）（3x+y）（x-2y）＝（）；

（5）（x-1）（x2+x+1）=（）