数据结构图结构.ppt

数据结构图结构.ppt

《数据结构图结构.ppt》由会员分享，可在线阅读，更多相关《数据结构图结构.ppt（74页珍藏版）》请在冰豆网上搜索。

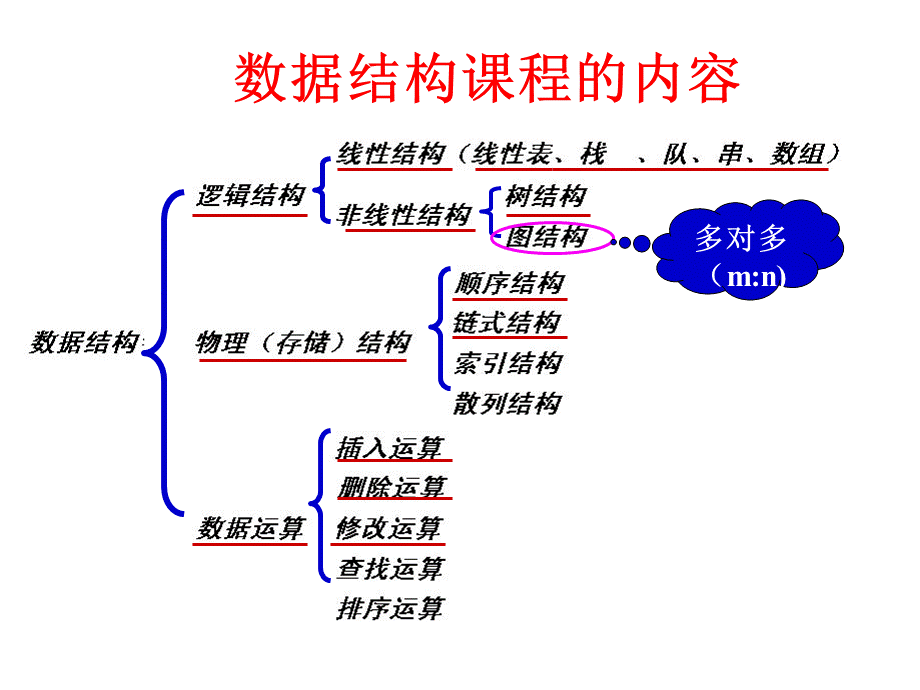
数据结构课程的内容,多对多（m:

n）,特点：

非线性结构，是研究数据元素之间的多对多的关系。

在这种结构中，任意两个元素之间可能存在关系。

即结点之间的关系可以是任意的，图中任意元素之间都可能相关。

图的应用极为广泛，已渗入到诸如语言学、逻辑学、物理、化学、电讯、计算机科学以及数学的其它分支。

第7章图,7.1基本术语7.2存储结构7.3图的遍历7.4图的其他运算7.5图的应用,第7章图,7.1图的基本术语,图：

记为G（V,E）其中：

V是G的顶点集合，是有穷非空集；E是G的边集合，是有穷集。

问：

当E（G）为空时，图G存在否？

答：

还存在！

但此时图G只有顶点而没有边。

有向图：

无向图：

完全图：

图G中的每条边都是有方向的；图G中的每条边都是无方向的；图G任意两个顶点都有一条边相连接；,若n个顶点的无向图有n（n-1）/2条边,称为无向完全图若n个顶点的有向图有n（n-1）条边,称为有向完全图,V=vertexE=edge,证明：

完全有向图有n（n-1）条边。

证明：

若是完全有向图，则顶点1必与所有其他顶点各有2条连线，即有2（n-1）条边，顶点2有2（n-2）条边，顶点n-1有2条边,顶点n有0条边.总边数2（n-1n-210）=2（n-1+0）n/2=n（n-1）,完全无向图有n（n-1）/2条边。

证明：

若是完全无向图，则顶点1必与所有其他顶点各有1条连线，即有n-1条边，顶点2有n-2条边，顶点n-1有1条边,顶点n有0条边.总边数n-1n-210=（n-1+0）n/2=n（n-1）/2,例：

判断下列4种图形各属什么类型？

无向,无向图（树）,有向图,有向,n（n-1）/2条边,n（n-1）条边,G1的顶点集合为V（G1）=0,1,2,3边集合为E（G1）=（0,1）,（0,2）,（0,3）,（1,2）,（1,3）,（2,3）,完全图,完全图,稀疏图：

稠密图：

设有两个图G（V,E）和G（V,E）。

若VV且EE,则称图G是图G的子图。

子图：

边较少的图。

通常边数n2边很多的图。

无向图中，边数接近n（n-1）/2；有向图中，边数接近n（n-1）,带权图：

即边上带权的图。

其中权是指每条边可以标上具有某种含义的数值（即与边相关的数）。

连通图：

在无向图中,若从顶点v1到顶点v2有路径,则称顶点v1与v2是连通的。

如果图中任意一对顶点都是连通的,则称此图是连通图。

非连通图的极大连通子图叫做连通分量。

带权图,在有向图中,若对于每一对顶点vi和vj,都存在一条从vi到vj和从vj到vi的路径,则称此图是强连通图。

非强连通图的极大强连通子图叫做强连通分量。

强连通图：

网络：

有两类图形不在本章讨论之列：

邻接点：

有向边（u,v）称为弧，边的始点u叫弧尾，终点v叫弧头,顶点v的度是与它相关联的边的条数。

记作TD（v）。

在有向图中,顶点的度等于该顶点的入度与出度之和。

顶点v的入度是以v为终点的有向边的条数,记作ID（v）;顶点v的出度是以v为始点的有向边的条数,记作OD（v）。

若（u,v）是E（G）中的一条边，则称u与v互为邻接顶点,弧头和尾：

度、入度和出度：

问：

当有向图中仅1个顶点的入度为0,其余顶点的入度均为1，此时是何形状？

TD（vi）顶点vi的度E图中边的个数N图中顶点的个数=E=1/2TD（vi）,答：

是树！

而且是一棵有向树！

生成树：

是一个极小连通子图，它含有图中全部顶点，但只有n-1条边。

如果在生成树上添加1条边，必定构成一个环。

若图中有n个顶点，却少于n-1条边，必为非连通图。

生成森林：

由若干棵生成树组成，含全部顶点，但构成这些树的边是最少的。

简单路径：

路径上各顶点v1,v2,.,vm均不互相重复。

回路：

例：

若路径上第一个顶点v1与最后一个顶点vm重合，则称这样的路径为回路或环。

路径：

在图G（V,E）中,若从顶点vi出发,沿一些边经过一些顶点vp1,vp2,vpm，到达顶点vj。

则称顶点序列（vivp1vp2.vpmvj）为从顶点vi到顶点vj的路径。

它经过的边（vi,vp1）、（vp1,vp2）、.、（vpm,vj）应当是属于E的边。

路径长度：

非带权图的路径长度是指此路径上边的条数；带权图的路径长度是指路径上各边的权之和。

ADTGraph数据对象V：

v是具有相同特性的数据元素的集合，称为顶点集。

数据关系R：

R=VR；VR=|v,wV且P（v,w）,表示从v到w的弧，谓词P（v,w）定义了弧的意义或信息基本操作P：

CreatGraph（初始条件：

图G存在，v和图中顶点有相同特征。

操作结果：

在图G中添加新顶点。

（参见P156-257）,图的抽象数据类型,注意：

V的大小写含义不同！

7.2图的存储结构,图的特点：

非线性结构（m:

n）,邻接表邻接多重表十字链表,设计为邻接矩阵,链式存储结构：

顺序存储结构：

无！

（多个顶点，无序可言）但可用数组描述元素间关系。

可用多重链表,重点介绍：

邻接矩阵（数组）表示法邻接表（链式）表示法,一、邻接矩阵（数组）表示法,建立一个顶点表（记录各个顶点信息）和一个邻接矩阵（表示各个顶点之间关系）。

设图A=（V,E）有n个顶点，则图的邻接矩阵是一个二维数组A.Edgenn，定义为：

例1：

邻接矩阵：

A.Edge=,（v1v2v3v4v5）,v1v2v3v4v5,0000000000000000000000000,分析1：

无向图的邻接矩阵是对称的；分析2：

顶点i的度第i行（列）中1的个数；特别：

完全图的邻接矩阵中，对角元素为0，其余全1。

0101010101010111010101110,0101010101010111010101110,顶点表：

例2：

有向图的邻接矩阵,分析1：

有向图的邻接矩阵可能是不对称的。

分析2：

顶点的出度=第i行元素之和，OD（Vi）=A.Edgeij顶点的入度=第i列元素之和。

ID（Vi）=A.Edgeji顶点的度=第i行元素之和+第i列元素之和,即：

TD（Vi）=OD（Vi）+ID（Vi）,邻接矩阵：

A.Edge=,（v1v2v3v4）,v1v2v3v4,0000000000000000,注：

在有向图的邻接矩阵中，第i行含义：

以结点vi为尾的弧（即出度边）；第i列含义：

以结点vi为头的弧（即入度边）。

顶点表：

0110000000011000,0110000000011000,容易实现图的操作，如：

求某顶点的度、判断顶点之间是否有边（弧）、找顶点的邻接点等等。

n个顶点需要n*n个单元存储边（弧）;空间效率为O（n2）。

对稀疏图而言尤其浪费空间。

特别讨论：

网（即有权图）的邻接矩阵,定义为：

以有向网为例：

邻接矩阵：

N.Edge=,（v1v2v3v4v5v6）,邻接矩阵法优点：

邻接矩阵法缺点：

顶点表：

5748956531,5748956531,注：

用两个数组分别存储顶点表和邻接矩阵#defineINFINITYINT_MAX/最大值#defineMAX_VERTEX_NUM20/假设的最大顶点数TypedefenumDG,DN,AG,ANGraphKind;/有向/无向图，有向/无向网TypedefstructArcCell/弧（边）结点的定义VRTypeadj;/顶点间关系，无权图取1或0；有权图取权值类型InfoType*info;/该弧相关信息的指针ArcCell,AdjMatrixMAX_VERTEX_NUMMAX_VERTEX_NUM;Typedefstruct/图的定义VertexTypevexsMAX_VERTEX_NUM;/顶点表，用一维向量即可AdjMatrixarcs;/邻接矩阵IntVernum,arcnum;/顶点总数，弧（边）总数GraphKindkind;/图的种类标志Mgraph;,图的邻接矩阵存储表示（参见教材P161）,对于n个顶点的图或网，空间效率=O（n2）,StatusCreateUDN（Mgraph/CreateUDN,例：

用邻接矩阵生成无向网的算法（参见教材P162）,对于n个顶点e条弧的网，建网时间效率=O（n2+n+e*n）,二、邻接表（链式）表示法,对每个顶点vi建立一个单链表，把与vi有关联的边的信息（即度或出度边）链接起来，表中每个结点都设为3个域；,每个单链表还应当附设一个头结点（设为2个域），存vi信息；,表结点,头结点,邻接点域，表示vi一个邻接点的位置,链域，指向vi下一个边或弧的结点,数据域，与边有关信息（如权值）,数据域，存储顶点vi信息,链域，指向单链表的第一个结点,每个单链表的头结点另外用顺序存储结构存储。

例1：

无向图的邻接表,邻接表,例2：

有向图的邻接表,邻接表（出边）,逆邻接表（入边）,注：

邻接表不唯一，因各个边结点的链入顺序是任意的。

例3：

已知某网的邻接（出边）表，请画出该网络。

80,64,1,2,5,当邻接表的存储结构形成后，图便唯一确定！

分析1:

对于n个顶点e条边的无向图，邻接表中除了n个头结点外，只有2e个表结点,空间效率为O（n+2e）。

若是稀疏图（en2），则比邻接矩阵表示法O（n2）省空间。

邻接表存储法的特点：

分析2:

在有向图中，邻接表中除了n个头结点外，只有e个表结点,空间效率为O（n+e）。

若是稀疏图，则比邻接矩阵表示法合适。

它其实是对邻接矩阵法的一种改进,怎样计算无向图顶点的度？

邻接表的缺点：

怎样计算有向图顶点的出度？

怎样计算有向图顶点的入度？

怎样计算有向图顶点Vi的度：

需遍历全表,邻接表的优点：

TD（Vi）=单链表中链接的结点个数,OD（Vi）单链出边表中链接的结点数ID（Vi）邻接点为Vi的弧个数,TD（Vi）=OD（Vi）+ID（Vi）,空间效率高；容易寻找顶点的邻接点；,判断两顶点间是否有边或弧，需搜索两结点对应的单链表，没有邻接矩阵方便。

讨论：

邻接表与邻接矩阵有什么异同之处？

1.联系：

邻接表中每个链表对应于邻接矩阵中的一行，链表中结点个数等于一行中非零元素的个数。

2.区别：

对于任一确定的无向图，邻接矩阵是唯一的（行列号与顶点编号一致），但邻接表不唯一（链接次序与顶点编号无关）。

邻接矩阵的空间复杂度为O（n2）,而邻接表的空间复杂度为O（n+e）。

3.用途：

邻接矩阵多用于稠密图的存储（e接近n（n-1）/2）；而邻接表多用于稀疏图的存储（en2）,图的邻接表存储表示（参见教材P163）,#defineMAX_VERTEX_NUM20/假设的最大顶点数TypedefstructArcNodeintadjvex;/该弧所指向的顶点位置structArcNode*nextarcs;/指向下一条弧的指针InfoArc*info;/该弧相关信息的指针ArcNode；TypedefstructVNode/顶点结构VertexTypedata;/顶点信息ArcNode*firstarc;/指向依附该顶点的第一条弧的指针VNode,AdjListMAX_VERTEX_NUM;Typedefstruct/图结构AdjListvertics;/应包含邻接表intvexnum,arcnum;/应包含顶点总数和弧总数intkind;/还应说明图的种类（用标志）ALGraph;/图结构,空间效率为O（n+2e）或O（n+e）时间效率为O（n+e*n）,它是有向图的另一种链式结构。

思路：

将邻接矩阵用链表存储，是邻接表、逆邻接表的结合。

1、每条弧对应一个结点（称为弧结点，设