spss多因素方差分析报告例子.docx

spss多因素方差分析报告例子.docx

《spss多因素方差分析报告例子.docx》由会员分享，可在线阅读，更多相关《spss多因素方差分析报告例子.docx（23页珍藏版）》请在冰豆网上搜索。

spss多因素方差分析报告例子

作业8：

多因素方差分析

1，data0806-height是从三个样方中测量的八种草的高度，问高度在三个取样地点，以及八种草之间有无差异？

具体怎么差异的？

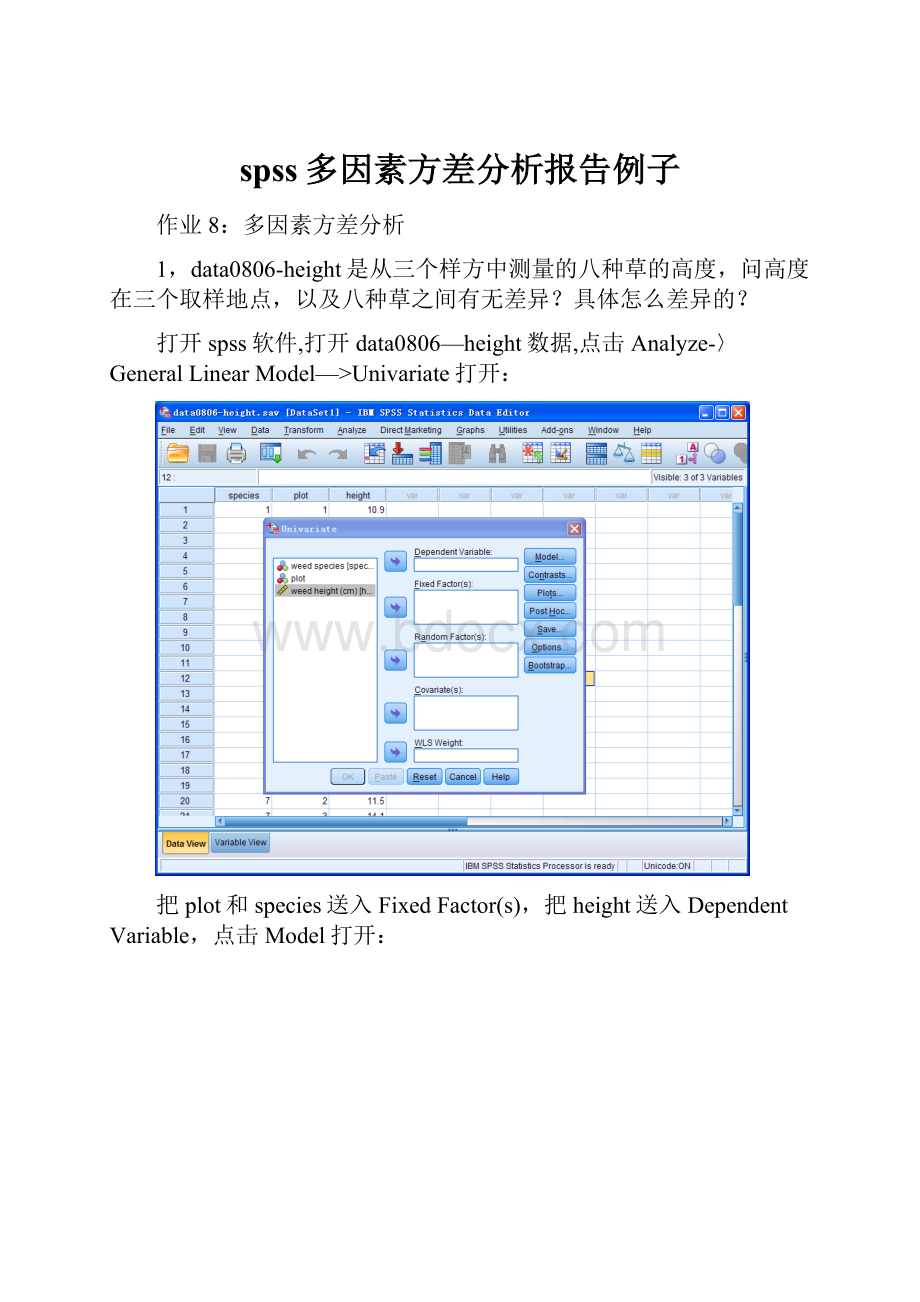
打开spss软件,打开data0806—height数据,点击Analyze-〉GeneralLinearModel—>Univariate打开：

把plot和species送入FixedFactor（s），把height送入DependentVariable，点击Model打开：

选择Fullfactorial,TypeIIISumofsquares，Includeinterceptinmodel（即全部默认选项），点击Continue回到Univariate主对话框,对其他选项卡不做任何选择,

结果输出:

因无法计算𝑀𝑀𝑒rror，即无法分开𝑀𝑀intercept和𝑀𝑀error，无法检测interaction的影响，无法进行方差分析，

重新Analyze—〉GeneralLinearModel—>Univariate打开：

选择好DependentVariable和FixedFactor（s）,点击Model打开:

点击Custom，把主效应变量species和plot送入Model框，点击Continue回到Univariate主对话框，点击Plots：

把date送入HorizontalAxis，把depth送入SeparateLines，点击Add，点击Continue回到Univariate对话框,点击Options：

把OVERALL,species，plot送入DisplayMeansfor框，选择Comparemaineffects，Bonferroni，点击Continue回到Univariate对话框，

输出结果:

可以看到：

SSspecies=33.165,dfspecies=7，MSspecies=4.738；SSplot=33。

165，dfplot=7，MSplot=4.738；SSerror=21.472，dferror=14，MSerror=1.534；

Fspecies=3.089，p=0.034〈0。

05；Fplot=12。

130，p=0。

005〈0。

01;

所以故认为在5%的置信水平上，不同样地,不同物种之间的草高度是存在差异的。

该表说明：

SSspecies=33.165，dfspecies=7,MSspecies=4。

738；SSerror=21。

472,dferror=14,MSerror=1。

534；Fspecies=3.089，p=0。

034<0.05;物种间存在差异:

SSplot=33.165，dfplot=7，MSplot=4.738;SSerror=21。

472，dferror=14，MSerror=1。

534；

Fplot=12.130,p=0。

005〈0.01;不同的物种间在差异：

由边际分布图可知:

类似结论：

草的高度在不同样地的条件之间有差异（Fplot=12。

130,p=0。

005〈0.01），具体是,样地一和样地三之间存在的差异最大；八种不同草的高度也存在差异（Fspecies=3.089，p=0.034<0.05）,具体是第四种草和第五种草的差异最大。

再次检验不同种类草的高度差异：

重新进行方差分析，Analyze-〉GeneralLinearModel—>Univariate：

把species送入FixedFactor（s），把high送入DependentVariable,点击Plots：

把species送入HorizontalAxis，点击Add，点击Continue回到Univariate，点击PostHoc（因为我们已经知道species效应显著）:

把species送入PostHocTestsfor框，选择Tukey,

输出结果：

各组均值从小到大向下排列。

最大的是第五组,最小的是第四组，其中有些种类草的高度存在差异，有些不存在。

再次检验不同样地草的高度差异：

过程和上相似：

结果如下

不同样地的草高度存在差异，其中一样地的草高度最短,3样地的草高度最高，且三组之间都存在差异。

2，data0807—flower，某种草的开花初期高度在两种温度和两个海拔之间有无差异？

具体怎么差异的？

多因素单因变量方差分析通过Analyze-〉GeneralLinearModel->Univariate实现，把因变量height送入DependentVariable栏,把因素变量temperature和attitude送入FixedFactor（s）栏

点击Model选项卡,打开：

选着fullfactorial,type3，点击）Includeinterceptinmodel。

点击Plots对话框，打开:

：

可选择attitude到HorizontalAxis，然后选择temperature到HorizontalAxis,再选择attitude到SeparateLines，Plots框显示attitude,temperature,attitude*temperature，

EstimatedMarginalMeans选择OVERALL,产生边际均值的均值Display框选择要输出的统计量，Descriptivestatistics描述统计量,Homogeneitytests方差齐性检验。

结果输出:

主效应各因素各水平以及样本量,

各水平的均值和标准差。

把样本分为四组,进行方差齐性检验,方差不一致。

可以看到：

SSaltitude=503。

167，dfaltitude=1，MSaltitude=503.167；SStemperature=1149。

798，dftemperature=1，MStemperature=1149。

798；SSinteraction=338。

486，dfinteraction=1，MSinteraction=338。

486；SSerror=935。

748，dferror=83,MSerror=935.748；Faltitude=44。

63，

p=0。

034〈0.001;Ftemperature=101.986,p=0.005<0.001；Ftemperature=101。

986，〈0.001;Finteraction=34.458，p<0.001;

所以故认为在0.1%的置信水平上，不同温度,不同海拔之间的草高度是存在差异的.

在四个样本总体中，在95％的置信区间，花的平均高度范围为137。

719到139。

172之间.

在海拔为3200米处，在95%的置信区间，花的平均高度范围为139。

852到141.920之间。

在海拔为3400米处,在95％的置信区间，花的平均高度范围为134.985到137。

036之间。

aititude各水平的边际均值的多重比较，在本试验中，事实上𝐻0:

平均aititude（3200）=aititude（3400）;但是平均aititude（3200）花高度—平均aititude（3400）花高度,在95％置信区间为3。

427到6.333。

故均值存在差异。

SSaltitude=503。

167，dfaltitude=1，MSaltitude=503.167；SSerror=935.748，dferror=83，MSerror=935.748；Faltitude=44.63，P〈0。

001。

不同海拔的花高度不存在差异的的概率＜0。

001。

在温度为T1处，在95％的置信区间,花的平均高度范围为141。

149到143。

119之间。

在温度为T2处，在95％的置信区间，花的平均高度范围为133.689到135.825之间。

温度各水平的边际均值的多重比较,在本试验中，事实上𝐻0：

（T1时，平均花高度）=（T2时,平均花高度）；但是（T1时，平均花高度）—（T2时，平均花高度）,在95％置信区间为5。

924到8.830,故均值存在差异，不接受H0假设.

SStemperature=1149.798，dftemperature=1，MStemperature=1149.798；SSerror=935.748，dferror=83，MSerror=935。

748；Ftemperature=101。

986,p<0.001;不同温度下，花的高度存在差异。

在温度为T1，海拔3200米处，在95%的置信区间，花的平均高度范围为145.433到148。

004之间。

在温度为T2处,海拔3200米处在95%的置信区间，花的平均高度范围为133.433到136.673之间。

在温度为T1处，海拔3400米处，在95%的置信区间,花的平均高度范围为136.057到139。

043之间。

在温度为T2处，海拔3400米处，在95%的置信区间，花的平均高度范围为133.068到135。

853之间。

不同海拔下的的边际均值图

两个因素的边际均值交互效应图,该图直线相互交叉（即斜率不一样）表明有交互效应。

结论如下：

某种草的开花初期高度在两种温度之间有差异（Ftemperature=101。

986，p〈0。

001;），T1时草的开花初期高度高于T2时草的开花初期高度。

某种草的开花初期高度在两种海拔之间有差异（Faltitude=44.63,P〈0.001。

），海拔3200时草的开花初期高度高于海拔3400时草的开花初期高度.

温度和海拔对草的开花初期高度的影响存在交互效应（Finteraction=34.458,p<0.001）。