SPSS使用入门.docx

SPSS使用入门.docx

《SPSS使用入门.docx》由会员分享，可在线阅读，更多相关《SPSS使用入门.docx（24页珍藏版）》请在冰豆网上搜索。

SPSS使用入门

SPSS在语言测试研究中的应用

1数据的输入与保存

1.1SPSS界面

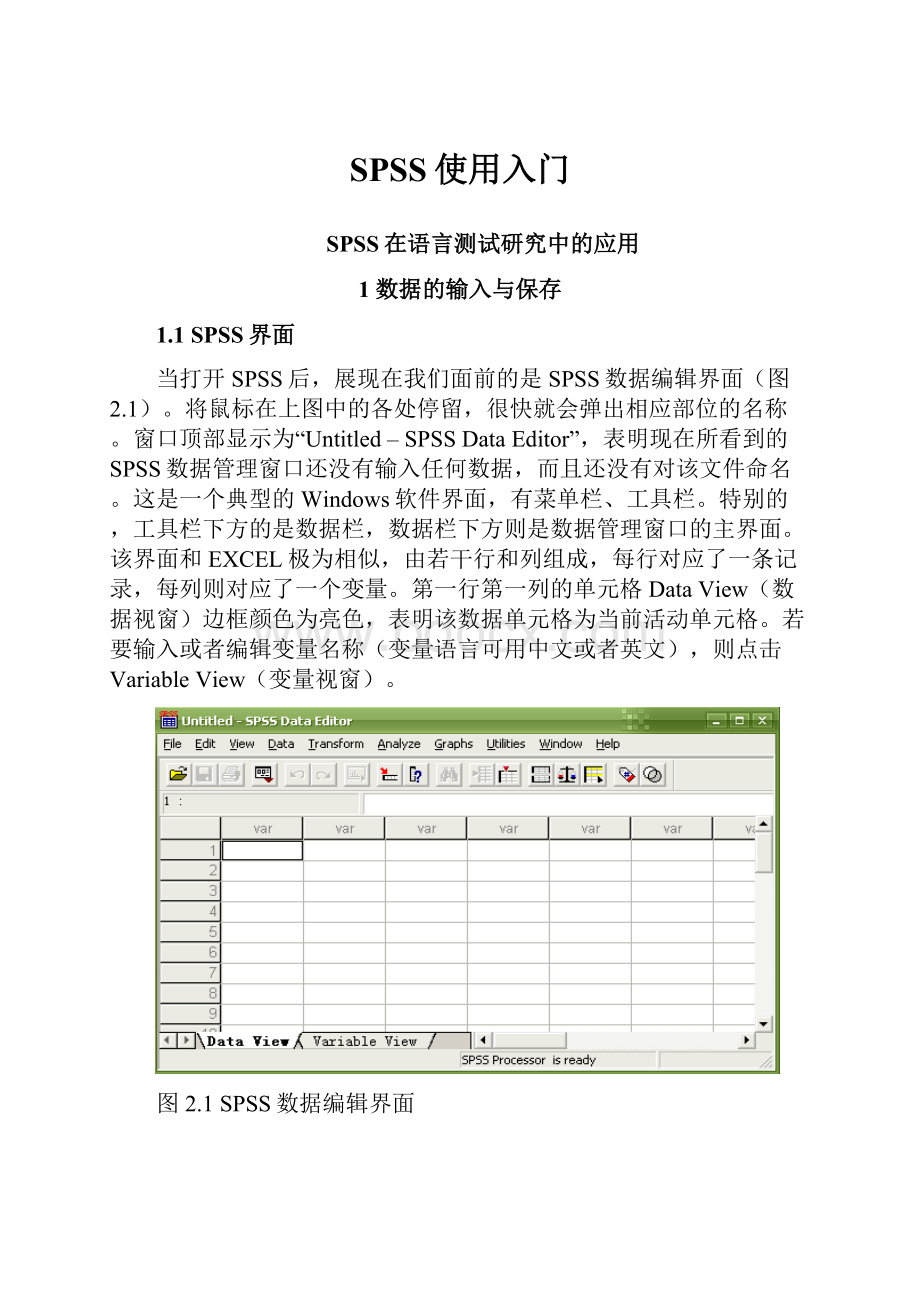
当打开SPSS后，展现在我们面前的是SPSS数据编辑界面（图2.1）。

将鼠标在上图中的各处停留，很快就会弹出相应部位的名称。

窗口顶部显示为“Untitled–SPSSDataEditor”，表明现在所看到的SPSS数据管理窗口还没有输入任何数据，而且还没有对该文件命名。

这是一个典型的Windows软件界面，有菜单栏、工具栏。

特别的，工具栏下方的是数据栏，数据栏下方则是数据管理窗口的主界面。

该界面和EXCEL极为相似，由若干行和列组成，每行对应了一条记录，每列则对应了一个变量。

第一行第一列的单元格DataView（数据视窗）边框颜色为亮色，表明该数据单元格为当前活动单元格。

若要输入或者编辑变量名称（变量语言可用中文或者英文），则点击VariableView（变量视窗）。

图2.1SPSS数据编辑界面

1.2定义变量

图2.2显示的是变量视窗编辑。

第一列是变量名称（Name），如id（调查对象的序号）从左到右依次为变量类型，系统默认的变量为数值型（Numeric），长度（Width）为8，有两位小数位（Decimals），标签，变量值（Values）。

变量值标签在右侧的Value框定义。

图2.2SPSS变量的定义

以group为例，单击Value框右半部的省略号，会弹出变量值标签对话框（图2.3）。

上部的两个文本框分别为变量值输入框和变量值标签输入框，分别在其中输入“1”和“20school”，此时下方的Add钮变黑，单击它，该变量值标签就会被加入下方的标签框内。

与此类似定义其他变量值，最后按OK按钮，变量值标签就设置完成。

此时你做任何分析，在结果中都有相应的标签出现。

图2.3SPSS变量值标签对话框

变量值后面的是缺失值定义，尚无缺失值（Missing）。

接下来的变量定义是显示对齐方式（Align）为右对齐，变量属性为数值变量（scale），也叫等距变量。

变量属性还包括分类变量，分为有序分类变量（Ordinal）和无序分类变量（Nominal）。

上图第一栏是第一个变量（id），通常用于定义外语测试研究中的参与对象，如考生和外语学习者。

第二栏是Group变量，用于对实验调查对象分类。

第三栏以下的变量为考试题目的变量名称，如n1（第1题），n2（第2题）等等。

1.3输入数据

接下来的任务是在数据视窗中依次输入数据（图2.4）。

图2.4中呈现的数据表示有30名考生，分成了五个小组，作答了8道多项选择题。

为了便于统计客观题的数据，通常用数字1表示正确作答，数字0表示错误作答。

图2.4SPSS的数据输入

1.4保存数据

选择菜单File==>Save，若该数据从来没有被保存过，会弹出Saveas对话框（图2.5）。

图2.5SPSS数据的保存

单击保存类型列表框，可以看到SPSS所支持的各种数据类型，有文本文件格式*.dat、EXCEL等等，这里我们仍然将其存为SPSS自己的数据格式（*.sav文件）。

在文件名框内键入itemanalysis并回车，可以看到数据管理窗口左上角由Untitled变为了图4的变量名itemanalysis。

2SPSS语言测试研究中的应用案例

2.1英语期末考试成绩的描述统计分析

内容：

制作成绩频数（分段：

0－60；60－70；70－80；80－90；90－100）分布表并作频数分布分析，计算平均值（mean），众数（mode），中数（median），标准差（Std.deviation），方差（variance），倾斜度（skewness），峰值（kurtosis），全距（range），总和（sum）

频数分布表是描述性统计最常用的方法之一，Frequencies过程就是专门为产生频数表而设计的。

它不仅可以产生详细的频数表，还可以按要求给出某百分位点的数值，以及常用的条、圆、图等统计图。

选择Analyze==>DescriptiveStatistics==>Descriptivestatistics==>Frequencies菜单，系统弹出描述对话框（图2.6）。

该对话框可分为左右两大部分，左侧为所有可用的侯选变量列表，右侧为选入变量列表。

我们只需要描述score，用鼠标选中score，单击中间的按钮，变量score的标签就会移入到右侧，注意这时OK按钮变黑，表明已经可以进行分析了。

图2.6Frequencies对话框的界面

需要分析的数据除了成绩的频数还有其他数据，所以下一步就点击Statistics，选择表示数据集中趋势（CentralTendency）的统计量Mean、Median、Mode、Sum，表示数据离散度（Dispersion）的Std.deviation、Variance、Range和表示数据分布（Distribution）的Skewness、Kurtosis。

点击Continue，回到刚才的视窗，点击Charts，选中Histograms了解数据的分布形状，依次选择Continue==>OK按钮，系统会弹出一个新的界面，生成所需的统计（图2.7）。

图2.7英语期末考试成绩的描述统计

图2.7窗口左上方的名称为SPSSViewer，即（结果）浏览窗口，整个的结构和资源管理器类似，左侧为导航栏，右侧为具体的输出结果。

结果表格给出了样本数、最小值、最大值、均数和标准差等这几个常用的统计量，以及我们所需的统计量。

从中可以看到，考生人数为80人，没有缺失的数据，所需描述统计的结果如表2.1。

人数

平均分

中数

众数

标准差

方差

倾斜度

峰值

全距

总和

80

85.48

86.50

89

5.827

33.949

-.993

.833

27

6838

表2.1英语期末考试成绩的描述统计

从表2.1可以看到，本次考试的平均分为85.48分，考试成绩最中间的分数（中数）是86.5，人数最多的分数（众数）是89，考生分数离平均分的标准距离（标准差）是5.827，分数构成的抛物线形态（倾斜度）为负偏态，斜度-.993，表示考生的英语成绩超过平均分85.48的人数比低于平均分的人数要多（图2.8）。

图2.8英语期末考试成绩的柱状分布图

表2.2是英语期末考试成绩的频数分布。

Frequency是每个分数出现的频数，Percent是该分数所占的百分比，CumulativePercent是该分数的累积百分比，指该考生分数在整个群体中的位置。

例如，某考生的分数为80，该分数的累积百分比为17.5%，那么该生的英语期末成绩只比17.5%的考生好。

根据各分数段包含的人数分及其所占的百分比，就可得出每个分数段的人数和比例。

Frequency

Percent

CumulativePercent

Valid

68

1

1.3

1.3

70

1

1.3

2.5

72

2

2.5

5.0

73

1

1.3

6.3

74

1

1.3

7.5

76

2

2.5

10.0

77

2

2.5

12.5

80

4

5.0

17.5

81

1

1.3

18.8

82

2

2.5

21.3

83

5

6.3

27.5

84

6

7.5

35.0

85

8

10.0

45.0

86

4

5.0

50.0

87

5

6.3

56.3

88

4

5.0

61.3

89

12

15.0

76.3

90

7

8.8

85.0

91

5

6.3

91.3

92

2

2.5

93.8

93

2

2.5

96.3

95

3

3.8

100.0

Total

80

100.0

表2.2英语期末考试成绩的频数分布

图2.9英语期末考试成绩的频数分布图

当然，考生成绩的频数分布图制作还可以采用另外一种方法。

选择菜单Transform==>Record==>IntoDifferentVariables，出现Recode对话框（图2.10）。

图2.10变量Recode对话框

将score选入InputVariable->OutputVariable框，此时OutputVariable框变黑，在其中键入新变量名group并单击Change，可见原来的score->?

变成了score->group。

单击“OldandNewValues”，系统弹出变量值定义对话框（图2.11）。

图2.11新旧变量的转换

按照题目的要求，选择Range:

Lowestthrough，在右侧框中键入60，然后在右上方的Value右侧框中键入对应的新变量值1，此时下方Add键变黑，单击它，Old->New框中就会加入Lowestthru60->1，按照类似的方法依次加入另外几条转换规则，最终Old->New框中共有Lowestthru60->1、160thru70->2、70thru80->3、80thru90->4、90thru100->5五条，现在单击Continue，再单击OK，系统就会按要求生成新变量group。

按照变量值标签对话框操作方法将1-5分别定义5个为分数段。

选择Analyze==>DescriptiveStatistics==>Descriptivestatistics==>Frequencies菜单，系统弹出描述频数的对话框如，将group变量移入到右侧，选点击Chart按钮，选择Barcharts（柱状图），ChartValues选Percentages（百分比），点击Continue按钮返回，点击OK按钮，系统生成所需的频数分布表（表2.3）和图（图2.12）。

这里的分数段统计包括了每段最高的分数，如60-70分数段包括分数为70的考生。

Frequency

Percent

Valid

60-70

2

2.5

70-80

12

15.0

80-90

54

67.5

90-100

12

15.0

Total

80

100.0

表2.3英语期末考试成绩的频数分布表

图2.12英语期末考试成绩的频数分布图

2.2英语试卷的项目分析

内容：

有30名考生，作答了8道多项选择题的英语试题，请计算每道题目的难度、区分度以及这套试题的信度

我们现在利用图2.4所提供的数据来分析。

选择Analyze==>Scale==>ReliabilityAnalysis菜单，系统弹出描述对话（图2.13）。

图2.13信度分析对话框

我们需要分析8道题目的难度、区分度以及这套试题的信度，用鼠标选中变量n1-n8，单击中间的按钮，这些变量的标签就会移入到右侧。

点击Statistics（统计），依次选中Item，Scaleifitemdeleted，选择Continue==>OK按钮，系统会弹出一个新的界面，生成所需的统计（图2.14）。

图2.14题目的难度、区分度和试题的信度系数

从图2.14可以看到n1的Mean为.9333，因为我们的计分方法是正确为1，错误为0，这个平均分就是第一道题目的难度，也叫易度指数（itemfacility），表示题目的容易程度。

一般认为，题目的难度介于0.3-0.7之间，难度在0.3以下的题目较难，这样的题目须修改；难度在0.7以上的题目较易，难度为0.5的题目最好。

不过，在课堂测验中，我们的测验目的是了解英语教学活动达到教学目标的程度，了解学生掌握学习目标的程度，若是学生掌握了题目所代表的全部知识和技能，则每道题目的难度为1。

这时，难度在0.7以上的题目表示学生对题目所代表的知识或技能掌握很好；难度在0.5以下的题目表示学生对题目所代表的知识或技能掌握很差，学生应该补习这种题目包含的知识或技能（Hudson&Lynch1984:

177）。

StdDev表示题目的标准差，8道题目中标准差最小的是第1题、第2题和第8题（StdDev=.2537），表示考生在这三道题目中的得分差异不大。

Cases指考生人数。

CorrectedItem-TotalCorrelation（题目-总分的校正相关系数）就是题目的区分度，表示题目能够区分优生和差生的程度。

8道题目中，区分度最好的题目是第3题，区分度为0.7193；区分度最差的题目是第2题，区分度为0.2614。

ReliabilityCoefficients指试题的信度系数。

系数越高，统计的误差越小。

一般认为，客观试题的信度系数在0.8以上，表示试题的误差较小，信度良好；0.9以上的信度系数为优秀；0.7-0.8的信度系数为中等；0.6-0.7的信度系数可以接受；试题信度在0.6以下则不可接受，试题须修改。

客观试题的信度与题目的难度和区分度有关，而区分度则和考生之间的差异性有关，考生的英语水平差异越大，题目的区分度越高，试题的信度就越高。

题目的数量越多，信度自然就越高。

本套试题的考生人数为30人，题目数为8，Alpha系数为0.7355。

区分度取舍的主要依据AlphaifItemDeleted（题目去掉后的信度系数），若一道题目去掉后，整套试题的信度在原来的基础上下降，说明此题对整套试题来讲很重要，区分度理想，反之说明该题目的区分度不理想，须修改或剔除。

从图2.14来看，每一道题目去掉后，试题的信度都会下降，这说明这些题目的区分度都理想。

2.3作文评阅的相关性和一致性分析

内容：

现有5名英语教师分别独立采用整体印象法评阅20名学生的作文，作文满分为10，数据为EXCEL文件（图2.15），分析不同评卷员之间的相关性和一致性。

图2.15EXCEL文件：

相关分析数据

在外语测试中经常要遇到分析两个或多个变量间关系的情况，有时是希望了解某个变量对另一个变量的影响强度，有时则是要了解变量间联系的密切程度，前者用回归分析来实现，后者则需要用相关分析实现。

要使用SPSS来做相关分析，我们需要将EXCEL文件导入到SPSS。

选择菜单File==>Open==>Data或直接单击快捷工具栏上的

按钮，系统就会弹出OpenFile对话框，单击“文件类型”列表框，在里面能看到直接打开的数据文件格式。

选中所需的EXCEL文件，如下图所示（图2.16），点击OK按钮，即可将其导入到SPSS中来，将文件保存。

图2.16非SPSS格式文件导入对话框

相关分析和其他推断统计分析一样，有参数检验和非参数检验两种。

参数检验至少需要满足两个条件：

样本量30以上，正态分布的数据。

若样本小于30或者数据不是正态分布，最好采用非参数检验。

数据正态分布检验方法如下：

选择Analyze==>NonparametricTests==>1-sampleK-Stest，系统弹出描述对话框（图2.17）。

图2.17正态分布检验对话框

TestDistribution选择，点击OK按钮，系统生成所需的统计结果（表2.4）。

RATER1

RATER2

RATER3

RATER4

RATER5

N

20

20

20

20

20

NormalParameters（a,b）

Mean

9.0900

8.7350

9.1900

8.7750

8.9750

Std.Deviation

.42785

.48507

.32102

.50770

.40377

MostExtremeDifferences

Absolute

.099

.271

.177

.171

.190

Positive

.091

.176

.138

.171

.118

Negative

-.099

-.271

-.177

-.149

-.190

Kolmogorov-SmirnovZ

.442

1.213

.791

.766

.848

Asymp.Sig.（2-tailed）

.990

.105

.558

.600

.469

aTestdistributionisNormal.

bCalculatedfromdata.

表2.4数据正态分布检验结果

表2.4显示五位评分员的评分数据服从正态分布，可以采用参数检验。

选择Analyze==>Correlate==>Bivariate，系统弹出描述对话框（图2.18）。

图2.18BivariateCorrelations对话框

此过程用于进行两个/多个变量间的参数/非参数相关分析，如果是多个变量，则给出两两相关的分析结果。

CorrelationCoefficients复选框组用于选择需要计算的相关分析指标。

Pearson复选框选择进行积差相关分析，即最常用的参数相关分析；Kendall'stau-b复选框计算Kendall's等级相关系数；Spearman复选框计算Spearman相关系数，即最常用的非参数相关分析（秩相关）。

TestofSignificance单选框组用于确定是进行相关系数的单侧（One-tailed）或双侧（Two-tailed）检验，一般选双侧检验。

Flagsignificantcorrelations用于确定是否在结果中用星号标记有统计学意义的相关系数，一般选中。

此时p<.05的系数值旁会标记一个星号，p<0.01的则标记两个星号。

本例采用Pearson积差相关分析方法，它满足以下两个条件：

（1）变量都是等距或者等比测量数据；

（2）变量所来自的总体是正态分布（张敏强2002：

58）。

依次将要分析的数据移入到右侧，选中CorrelationCoefficients（相关系数）分析中的Pearson方法，采用默认的显著性检验（TestofSignificance）方法Two-tailed（双侧检验），点击OK按钮，系统会弹出一个新的界面，生成所需的统计（表2.5）。

RATER1

RATER2

RATER3

RATER4

RATER5

RATER1

1

.605（**）

.555（*）

.554（*）

.660（**）

.005

.011

.011

.002

20

20

20

20

RATER2

1

.423

.393

.392

.063

.087

.088

20

20

20

RATER3

1

.308

.599（**）

.186

.005

20

20

RATER4

1

.418

.067

20

RATER5

1

**Correlationissignificantatthe0.01level（2-tailed）.

*Correlationissignificantatthe0.05level（2-tailed）.

表2.5作文评分者之间的相关系数

从表2.5来看，评分员之间的相关差异较大。

RATER1和其他四个作文评阅人的评分存在显著相关，相关系数比较理想。

RATER的作文评分除了与RATER1的显著相关外，与其他三人的评分结果都不相关。

RATER3的评分仅和第一个和第五个评阅人相关。

RATER4和RATER5的作文评分仅和第一个评阅人相关。

这说明五位作文评阅教师之间的相关并不理想，对作文的评判标准和学生的作文理解差异较大，评分员之间的一致性应该不理想。

评分员之间的一致性相当于客观试题的信度系数，评分员对每篇作文的理解一致，则评分误差小，评分结果的可信性度高；反之误差大，评分结果的可信度低。

评分员之间的一致性取决于每位评分者对评分标准的把握和对考生作文水平的理解是否一致。

若评分员在评阅过程中，评分标准滥用，前后评阅不一致，就会导致评分员内部一致性差；若和其他评分员之间的差异太大，就会导致外部一致性差，即评分员之间的一致性差。

请注意，统计评分员之间的一致性的数据输入方法和相关系数的数据输入方法不一样，如下所示（图2.19）。

图2.19非参数肯德尔和谐系数统计的数据输入

选择菜单Analyze==>NonparametricTests==>KRelatedSamples进入多列相关样本检验的对话框（图2.20）。

图2.20TestsforSeveralRelatedSamples对话框

检验类型有三种：

Friedman检验，Kendall’sW检验和Cochran’sQ检验。

Friedman检验等同于参数检验中单个样本的重复设计或者方差分析，该检验测试K个相关变量是否来自同一总体的零假设。

Kendall’sW检验可解释成协同系数，是Friedman检验的标准化形式，它测量评分者之间的一致性，该检验的变量是评分者评判的题目或者考生。

Cochran’sQ检验测试多个相关两分变量（如作答正确记为1，错误记为0的变量）是否有相同的平均分，该检检验的变量可以是同一个体或者相匹配的个体。

将所测变量移入到右侧，选择Kendall协同系数检验法，按OK按钮，系统生成所需统计结果（表2.6）。

从表2.6看到，此次的评分人员有5个，Kendall协同系数为.523，卡方值为49.668，自由度为19，p<.01。

这表明评分员之间的一致性程度具有统计意义，但是一致性程度不高。

为了提高评分员之间的一致性，我们需要做许多工作，如加强阅卷教师的培训，使其掌握评分标准；加强试卷的保密性；制定合乎规范、可操作性强的评分细则；增加试卷复评等等。

N

5

Kendall'sW（a）

.523

Chi-Square

49.668

df

19

Asymp.Sig.

.000

Kendall'sCoefficientofConcordance

表2.6评分者之间的一致性结果：

Kendall协同系数

2.4高考分数与作文分数的线性回归分析

内容：

现有20名考生的高考作文成绩和高考总分，试分析高考作文和高考总分的线性回归关系。

图2.21是20名考生的高考成绩和作文成绩数据

图2.2120名考生的高考成绩和作文成绩

回归分析和相关分析一样也是对变量依存关系的分析。

一般来说，相关程度越高，回归分析的结果就越可靠，在做回归分析之前，先做相关分析以此作为判别回归分析结果的一个重要依据。

相比而言，相关分析探讨变量之间的共变关系，即非因果关系，而回归分析则区分变量之间的因果关系。

相关分析检验变量之间的关系的密切程度，而回归分析对具有相关关系的变量建立回归模型来描述变量之间的具体变动关系，通过控制或者给定自变量的数值来估计或者预测因变量的数值。

在进行回归分析之前，我们最好制作散点图来表现高考作文和高考总分之间有无相关关系。

散点图用点的密集程度和趋势表示两个变量之间的相关关系与变化趋势（张文彤、闫洁2004：

201）。

图2.22散点图预定义对话框

在SPSS中有四种散点图（图2.22），即用于两个变量之间关系的简单散点图、多个变量之间两辆相关