全国高考理科数学试题及答案北京卷.docx

全国高考理科数学试题及答案北京卷.docx

《全国高考理科数学试题及答案北京卷.docx》由会员分享，可在线阅读，更多相关《全国高考理科数学试题及答案北京卷.docx（9页珍藏版）》请在冰豆网上搜索。

全国高考理科数学试题及答案北京卷

2016年普通高等学校招生全国统一考试

数学（理）（北京卷）

本试卷共5页，150分．考试时长120分钟．考生务必将答案答在答题卡上，在试卷上作答无效．考试结束后，将本试卷和答题卡一并交回．

第一部分（选择题共40分）

一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．

（1）已知集合A=B=，则

（A）（B）

（C）（D）

（2）若x,y满足，则2x+y的最大值为

（A）0（B）3

（C）4（D）5

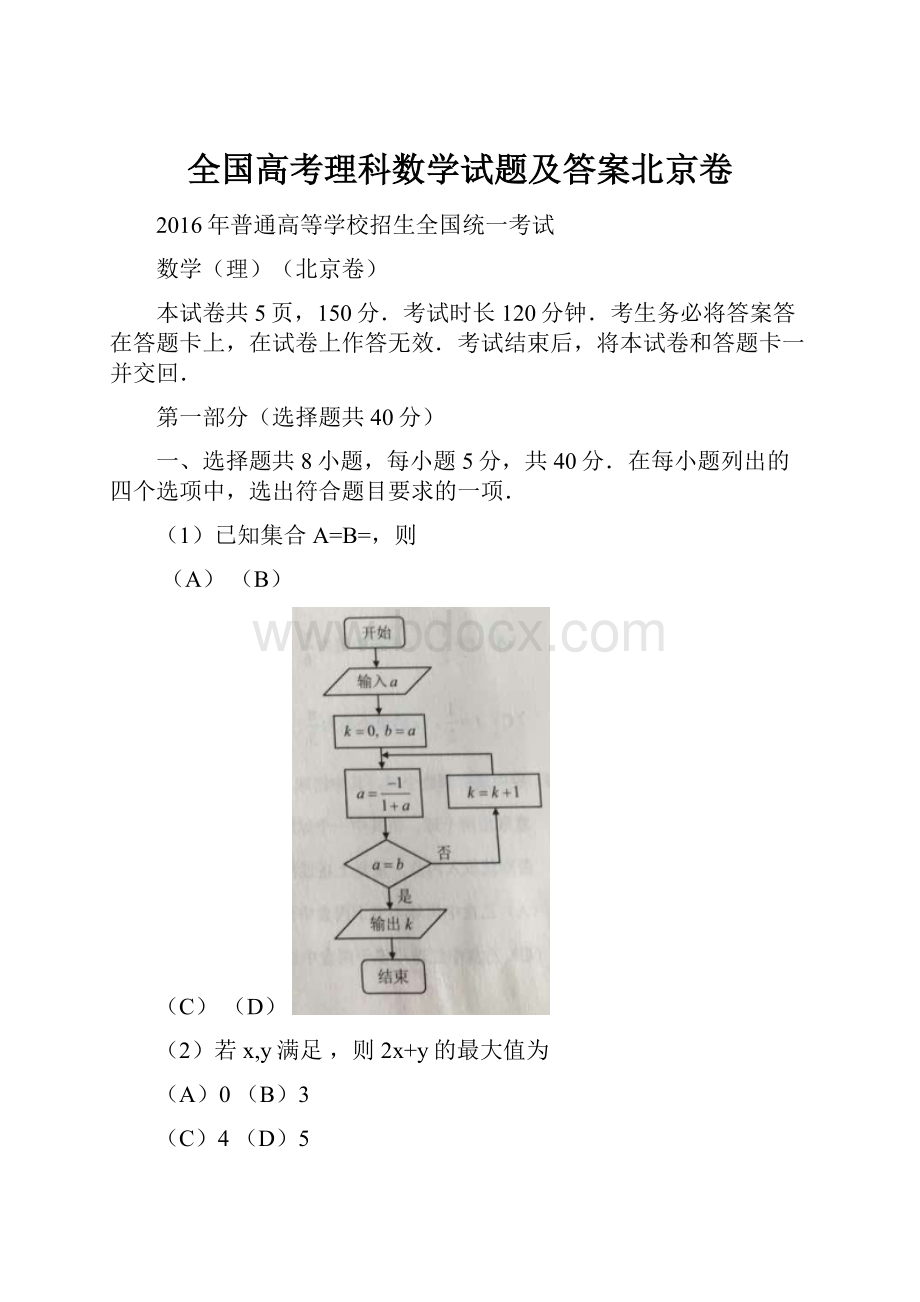
（3）执行如图所示的程序框图，若输入的a值为1，则输出的k值为

（A）1

（B）2

（C）3

（D）4

（4）设a,b是向量，则“IaI=IbI”是“Ia+bI=Ia-bI”的

（A）充分而不必要条件（B）必要而不充分条件

（C）充分必要条件（D）既不充分也不必要条件

（5）已知x,yR,且xyo，则

（A）-（B）

（C）（-0（D）lnx+lny

（6）某三棱锥的三视图如图所示，则该三棱锥的体积为

（A）

（B）

（C）

（D）1

（7）将函数图像上的点P（，t）向左平移s（s﹥0）个单位长度得到点P′.若P′位于函数的图像上，则

（A）t=，s的最小值为（B）t=，s的最小值为

（C）t=，s的最小值为（D）t=，s的最小值为

（8）袋中装有偶数个球，其中红球、黑球各占一半.甲、乙、丙是三个空盒.每次从袋中任意取出两个球，将其中一个球放入甲盒，如果这个球是红球，就将另一个球放入乙盒，否则就放入丙盒.重复上述过程，直到袋中所有球都被放入盒中，则

（A）乙盒中黑球不多于丙盒中黑球

（B）乙盒中红球与丙盒中黑球一样多

（C）乙盒中红球不多于丙盒中红球

（D）乙盒中黑球与丙盒中红球一样多

第二部分（非选择题　共110分）

二、填空题共6小题，每小题5分，共30分．

（9）设aR，若复数（1+i）（a+i）在复平面内对应的点位于实轴上，则a=_______________。

（10）在的展开式中，的系数为__________________.（用数字作答）

（11）在极坐标系中，直线与圆交于A，B两点，则=____________________.

（12）已知为等差数列，为其前n项和，若，，则.

（13）双曲线的渐近线为正方形OABC的边OA，OC所在的直线，点B为该双曲线的焦点。

若正方形OABC的边长为2，则a=_______________.

（14）设函数

若a=0，则f（x）的最大值为____________________；

若f（x）无最大值，则实数a的取值范围是_________________。

三、解答题（共6小题，共80分．解答应写出文字说明，演算步骤或证明过程）

（15）（本小题13分）

在

ABC中，

（I）求

的大小

（II）求

的最大值

（16）（本小题13分）A、B、C三个班共有100名学生，为调查他们的体育锻炼情况，通过分层抽样获得了部分学生一周的锻炼时间，数据如下表（单位：

小时）；

A班

66.577.58

B班

6789101112

C班

34.567.5910.51213.5

（

）试估计C班的学生人数；

（

）从A班和C班抽出的学生中，各随机选取一人，A班选出的人记为甲，C班选出的人记为乙，假设所有学生的锻炼时间相对独立，求该周甲的锻炼时间比乙的锻炼时间长的概率；

（

）再从A、B、C三个班中各随机抽取一名学生，他们该周的锻炼时间分别是7，9，8.25（单位：

小时），这3个新数据与表格中的数据构成的新样本的平均数记，表格中数据的平均数记为，试判断和的大小，（结论不要求证明）

（17）（本小题14分）

如图，在四棱锥P-ABCD中，平面PAD

平面ABCD，PA

PD,PA=PD,AB

AD,AB=1,AD=2,AC=CD=

（I）求证：

PD

平面PAB;

（II）求直线PB与平面PCD所成角的正弦值；

（III）在棱PA上是否存在点M，使得BMll平面PCD?

若存在，求

的值；若不存在，说明理由。

（18）（本小题13分）

设函数f（x）=xe

+bx，曲线y=f（x）dhko（2,f

（2））处的切线方程为y=（e-1）x+4，

（I）求a,b的值；

（II）求f（x）的单调区间。

（19）（本小题14分）

已知椭圆C：

（a>b>0）的离心率为

，A（a,0）,B（0,b），O（0，0），△OAB的面积为1.

（I）求椭圆C的方程；

（II）设P的椭圆C上一点，直线PA与Y轴交于点M，直线PB与x轴交于点N。

求证：

lANl

lBMl为定值。

（20）（本小题13分）

设数列A：

，

…

（N≥2）。

如果对小于n（2≤n≤N）的每个正整数k都有

＜

，则称n是数列A的一个“G时刻”。

记“G（A）是数列A的所有“G时刻”组成的集合。

（I）对数列A：

-2，2，-1，1，3，写出G（A）的所有元素；

（II）证明：

若数列A中存在

使得

>

，则G（A）

；

（III）证明：

若数列A满足

-

≤1（n=2,3,…,N）,则G（A）的元素个数不小于

-

。