管理系统工程习题培训讲学.docx

管理系统工程习题培训讲学.docx

《管理系统工程习题培训讲学.docx》由会员分享，可在线阅读，更多相关《管理系统工程习题培训讲学.docx（22页珍藏版）》请在冰豆网上搜索。

管理系统工程习题培训讲学

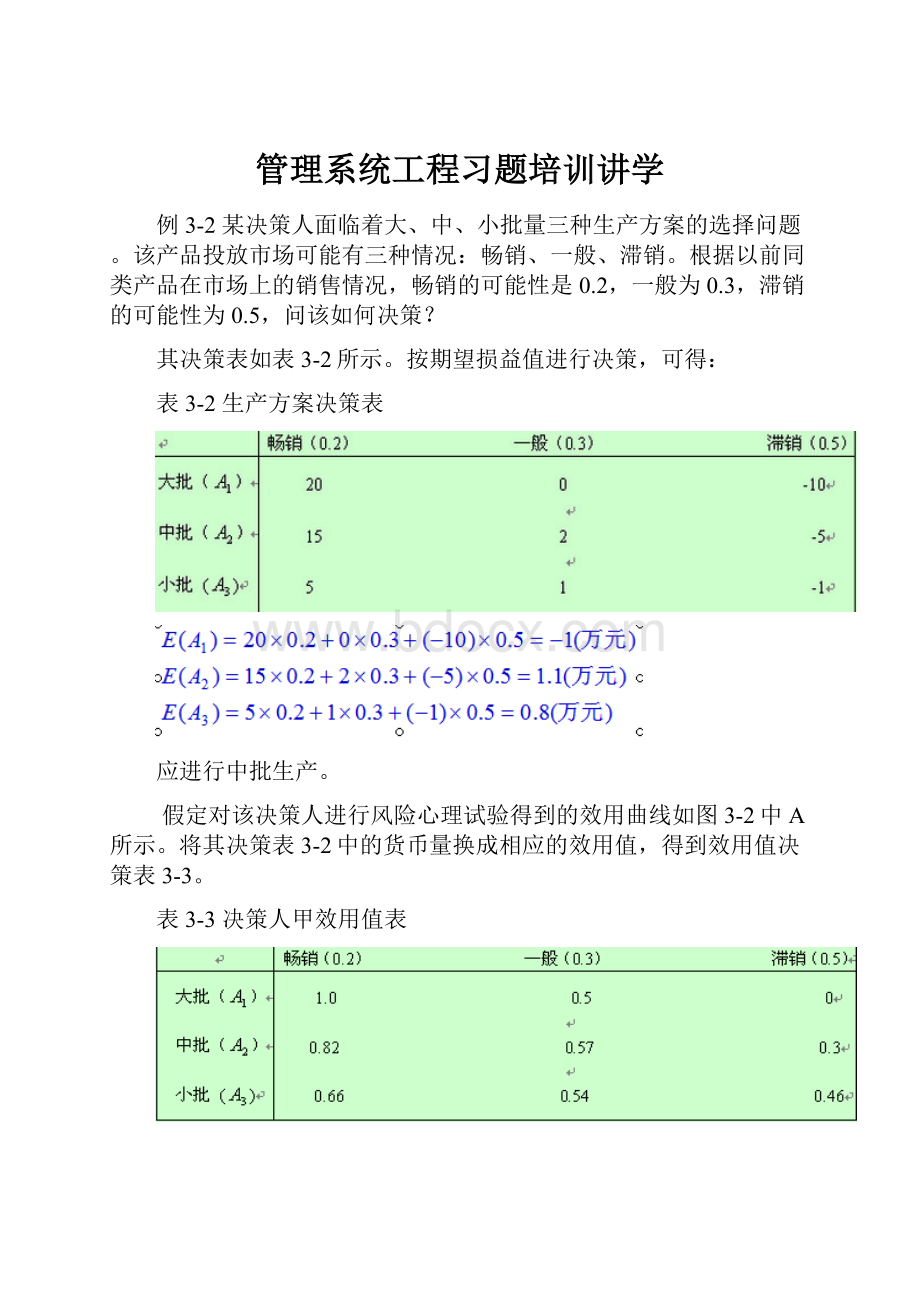
例3-2某决策人面临着大、中、小批量三种生产方案的选择问题。

该产品投放市场可能有三种情况：

畅销、一般、滞销。

根据以前同类产品在市场上的销售情况，畅销的可能性是0.2，一般为0.3，滞销的可能性为0.5，问该如何决策？

其决策表如表3-2所示。

按期望损益值进行决策，可得：

表3-2生产方案决策表

应进行中批生产。

假定对该决策人进行风险心理试验得到的效用曲线如图3-2中A所示。

将其决策表3-2中的货币量换成相应的效用值，得到效用值决策表3-3。

表3-3决策人甲效用值表

应采取小批量生产，这说明决策甲是小心谨慎的，是为保守

型决策人。

假定对该决策人进行风险心理试验得到的效用曲线如图3-2中曲线B所示。

将决策表中的货币量换成相应的效用值，得到效用值决策表3-4。

表3-4决策人乙效用值表

对决策人乙来说应选大批量生产，显然这是位敢冒风险的决策人。

例3-3某公司准备引进某新设备进行生产，这种新设备具有一定的先进性，但该公司尚未试用过，预测应用时成功的概率为0.8，失败的概率为0.2。

现有三种方案可供选择：

方案Ⅰ，应用老设备，可稳获4万元收益；方案Ⅱ，先在某一车间试用新设备，如果成功，可获7万元收益，如果失败则将亏损2万元；方案Ⅲ，全面推广使用新设备，如果成功，可获12万元收益，如果失败则亏损10万元，试问该公司采取哪种方案？

解：

（1）如果采用货币期望值标准，可画出决策树如图3-3所示：

由决策值可知，该公司应采取方案Ⅲ为最优方案，因为方案Ⅲ收益期望值为最大（7.6万元）。

但是，可以看到，若采取方案Ⅲ，必须冒亏损10万元的风险，虽然亏损的概率较小，但仍有可能发生。

对这个决策问题不同的人有不同的态度。

（1）如果该公司资金较少，亏损10就意味着因资金无法周转而停产，甚至倒闭。

那么公司领导一般不会采取方案Ⅲ，而采取收益期望值较低的方案Ⅰ或Ⅱ。

（2）如果公司资金力量雄厚，经受得起亏损10万元的打击，公司领导又是富有进取心的，那么他可能会采取方案Ⅲ。

鉴于以上种种情况，有时以效用作为标准进行决策比以损益值进行决策更加切合实际。

（2）求决策值的效用曲线

规定最大收益（12万元）时，效用值为1，亏损最大（-10万元）时，效用值为0，用标准测定法向决策者提出一系列问题，找出对应于损益值的效用值，即可绘制出该决策值对此决策的效用曲线，如图3-3所示。

在所得曲线上可找到对应于各易损值的效用值：

4万元的效应值为0.94；

7万元的效用值为0.98；

12万元的效用值为1；

-2万元的效用值为0.70；

-10万元的效用值为0.00；

现用效用值进行决策：

方案Ⅰ的效用期望值为：

0.94

方案Ⅱ的效用期望值为：

方案Ⅲ的效用期望值为：

于是可得如下决策树，如图3-4所示：

由此可见，以效用值作为决策标准，应选方案Ⅰ。

这与损益期望值法的结论不一致，原因在于决策者对风险持慎重态度，是保守型决策者。

例3-5某市果品公司准备组织新年（双节）期间柑橘的市场供应，供应时间预计为70天。

根据现行价格水平，假如每公斤柑橘进货价格为3元，零售价格位4元，每公斤的销售纯收益为1元。

零售经营新鲜果品，一般进货和销售期为一周（7天），如果超过一周没有卖完，便会引起保管费和腐烂损失的较大上升。

如果销售时间超过一周，平均每公斤损失0.5元。

根据市场调查，柑橘销售量与当前其他水果的供应和销售情况有关。

如果其他水果供应充分，柑橘销售量将为6000公斤；如果其他水果供应销售不足，则柑橘日销售量将为8000公斤；如果其他水果供应不足进一步加剧，则会引起价格上升，则柑橘的日销售量将达到10000公斤。

调查结果显示，在此期间，水果储存和进货状况将引起水果市场如下变化：

5周时其他水果价格上升，3周时其他水果供应稍不足，2周时其他水果充分供应。

现在需提前两个月到外地订购柑橘，由货源地每周发货一次。

根据以上情况，该公司确定进货期为一周，并设计了3种进货方案：

A1：

进货方案为每周进货10000×7=70000（公斤）；

A2：

进货方案为每周进货8000×7=56000（公斤）；

A3：

进货方案为每周进货6000×7=42000（公斤）。

在“双节”到来之前，公司将决策选择哪种进货方案，以便做好资金筹集和销售网点的布置工作。

解：

分析原问题，柑橘的备选进货方案共有3个，每个备选方案面临3种自然状态，因此，由决策点出发，右边连出3条方案枝，末端有3个状态节点，每个节点分别引出3条概率枝，在概率枝的末端有9个结果点，柑橘日销售量10000公斤、8000公斤、6000公斤的概率分别为0.5、0.3、0.2.将有关数据填入决策树种，如图3-2所示。

分别计算状态节点②③④处的期望收益值，并填入如3-2中。

节点②:

70000×0.5+49000×0.3+28000×0.2=55300

节点③：

56000×0.5+56000×0.3+35000×0.2=51800

节点④：

42000×0.5+42000×0.3+42000×0.2=42000

比较状态节点处的期望收益值，节点②处最大，故应将方案枝A2、A3剪枝，留下A1分支，A1方案即每周进货70000公斤为最优方案。

例3-6某企业为了生产某种新产品，决定对一条生产线的技术改造问题拟出两种方案，一是全部改造，二是部分改造啊。

若采用全部改造方案，需投资280万元；若采用部分改造方案只需投资150万元。

两个方案的试用期都是10年。

估计在此期间，新产品销路好的概率是0.7，销路不好的概率是0.3，两个改造方案的年度损益值如表3-6所示。

请问该企业的管理者应如何决策改造方案。

例3-7如果对例3-6中的问题分为前4年后6年两期考虑，根据市场调查研究及预测分析，前4年新产品销路好的概率为0.7，而前4年销路好后6年销路也好的概率为0.9；但若前4年销路差，则后6年销路也差的概率为0.6。

在这种情况下，企业的管理者采用生产线全部改造和部分改造哪个方案更好些？

解：

决策步骤如下：

（1）绘制决策树，如图3-4所示。

（2）计算各节点处的期望收益值。

对于较复杂的决策问题，计算期望收益值时是由右向左，先计算后6年的期望损益值：

节点④：

[100×0.9+（-30）×0.1]×6=522

节点⑤：

[100×0.4+（-30）×0.6]×6=132

节点⑥：

（45×0.9+10×0.1）×6=249

节点⑦：

（45×0.4+10×0.6）×6=144

再计算前4年的期望损益及10年的净收益：

节点②：

[100×0.7+（-30）×0.3]×4+522×0.7+132×0.3-280=369（万元）

节点③：

（45×0.7+10×0.3）×4+249×0.7+144×0.3-150=205.5（万元）

（3）剪枝决策。

由以上计算可以看出，采用A1对生产线全部改造的方案可得净收益为369万元，采取A2部分改造方案可得净收益为205.5万元，因此，应选择全部改造为最佳方案，即保留全部改造方案枝，剪掉部分改造方案枝。

例3-8某连锁店经销商准备在一个新建居民小区兴建一个新的连锁店，经市场行情分析与推测，该店开业的头3年，经营状况好的概率为0.75，营业差的概率为0.25；如果头3年经营状况好，后7年经营状况也好的概率可达0.85；但如果头3年经营状态差后7年经验状态好的概率仅为0.1，差的概率为0.9。

兴建连锁店的规模有两个方案：

一是建中型商店。

二是先建小型商店，若前3年经营效益好，再扩建为中型商店。

各方案年均收益及投资情况如表3-7所示。

该连锁店管理层应如何决策？

解：

决策分析步骤：

（1）根据问题，绘制决策树，如图3-5所示。

（2）计算各节点及决策点的期望损益值。

从右向左，计算每个节点处的期望损益值，并将计算结果填入图3-5的相应各节点处。

节点⑧：

（150×0.85+10×0.15）×7-210=693

节点⑨：

（60×0.85+2×0.15）×7=359.1

对于决策点⑥来说，由于扩建后可得净收益693万元，而不扩建只能得净收益359.1万元。

因此，应选择扩建方案，再决策点⑥处可得收益693万元，将不扩建方案枝剪掉。

节点⑥：

693

节点④：

（150×0.85+10×0.15）×7=903

节点⑤：

（150×0.1+10×0.9）×7=168

节点⑦：

（60×0.1+2×0.9）×7=54.6

节点②：

（100×0.75+10×0.25）×3+903×0.75+168×0.25-400=551.75

节点③：

（60×0.75+2×0.25）×3+54.6×0.25+693×0.75-150=519.9

（3）剪枝决策。

比较放个方案可以看出，建中型商店可获净收益551.75万元。

先建小商店，若前3年效益好再扩建，可得净收益519.9万元，因此，应该选择建中型商店的方案为最佳方案，对另一个方案进行剪枝。

为进一步摸清市场对这种产品的需求情况，工厂通过调查和咨询等方式得到一份市场调查表。

销售情况也有好

表3-9销售情况概率

假定得到市场调查表的费用为万元，试问：

（1）补充信息（市场调查表）价值多少？

（2）如何决策可以使利润期望值最大？

、

第三步，验后分析。

Ø综上所述，如果市场调查费用不超过1.56万元，就应该进行市场调查，从而使企业新产品开发决策取得较好的经济效益。

如果市场调查费用超过1.56万元，就不应该进行市场调查。

Ø该企业进行市场调查，如果销路好，就应该选择生产；

Ø如果销路情况中等，也应该生产；如果销路差，就选择不生产。

例3-10某厂生产某种产品，若市场畅销，可以获得利润15000元，若市场滞销，将亏损5000元。

根据以往的市场调查情况，该产品畅销的概率为0.8，滞销的概率为0.2。

为了准确地掌握该产品的销售情况，可以聘请某咨询公司进行市场调查和分析，它对产品畅销预测的准确率为0.95，滞销预测的准确率为0.9。

如果咨询公司预测市场畅销，那么是否应该生产？

如果预测为滞销，是否应该进行生产？

解：

先验分布如表3-12所示

表3-12先验分布表

现在用H1和H2分别表示咨询公司提供畅销和滞销这两个情况

表3-13预测似然分布表

后验分布表和预测为情况下的后验分布决策表如表3-14和表3-15

在这种情况下，补充的情报使不确定问题变成确定问题。

如果H2是完全情报，决策者掌握了就会选择行动a2，即不生产，这时收益为0；如果决策者无此情报，那么就会按先验分布而选择行动a1，这时要损失5000元。

因此掌握此情报的收益提高5000元。

5000是完全情报H2的价值。

如果H1是完全情报，决策者掌握它选择行动a1，收益为15000。

未掌握它按先验分布决策也是a1，收益也是15000.因此掌握此完全情报的收益是0（元）。

在完全情报情况下进行决策，完全情报的价值的期望值称为完全情报价值，可表示为EVPI。

例题3-11，例3-10计算咨询公司提供的补充信息价值。

例3-11某厂打算处理一批库存产品，这些产品每箱100个，以箱为单位销售，已知这批产品每箱的废品率有三种可能20%，10%，5%，对应的概率分别为0.5，0.3，0.2。

假设该产品正品每箱市场价格为100元，废品不值钱。

现处理价格为每箱85元，遇到废品不予更换。

请对是否购买进行决策，如果允许抽取4个元件进行检验，确定所含废品个数，假定检验是允许放回的，如何进行决策？

试分析：

（1）如果不咨询，应如何生产？

（2）是否应该进行咨询后生产？

（3）计算完全情报价值。

（4）计算补充情报价值。

解：

（1）如果不咨询，由期望值准则

所以，应该采取大批生产方案。

（2）如果咨询，由全概率公式，分别求出咨询后销售状态结果值

再由贝叶斯公式

例3-12某工厂打算在甲和乙两种产品中选择一种进行生产。

根据以往的经验，如果在市场不发生变化的情况下，生产甲产品，可获得利润50万元；生产乙产品，要亏损15万元。

如果在市场条件发生变化的情况下，生产甲产品，会亏损20万元；而生产乙产品，可获得利润100万元。

根据以往的资料，预测市场不发生变化的概率是0.7，发生变化的概率是0.3.问应该如何决定生产哪种产品？

解：

先列出状态概率和损益值如表3-18所示。

表3-18状态概率和损益值

计算各方案的期望收益：

显然，生产甲产品为最优方案

假设市场不发生变化的概率从0.7变到0.8，这时两方案的期望利润：

显然，生产甲仍为最优方案

再假设市场不发生变化的概率由0.7变到0.6。

这时两方案的期望利润

这时，生产乙产品为最优方案。