树图.docx

树图.docx

《树图.docx》由会员分享，可在线阅读，更多相关《树图.docx（10页珍藏版）》请在冰豆网上搜索。

树图

第三讲树（Tree）

树型结构是一类重要的非线性结构，树型结构是结点之间有分支，并具有层次关系的结构，它非常类似于自然界中的树。

树型结构在客观世界中是大量存在的，例如家谱、行政组织结构都可用树形象的表示。

树在计算机领域中也有着广泛的应用，例如在编译程序中，用树来表示源程序语法结构；在数据库系统中，可以用树来组织信息。

从本讲开始重点讲解什么是树和二叉树，下一讲将和大家共同讨论二叉树遍历。

一、树的概念：

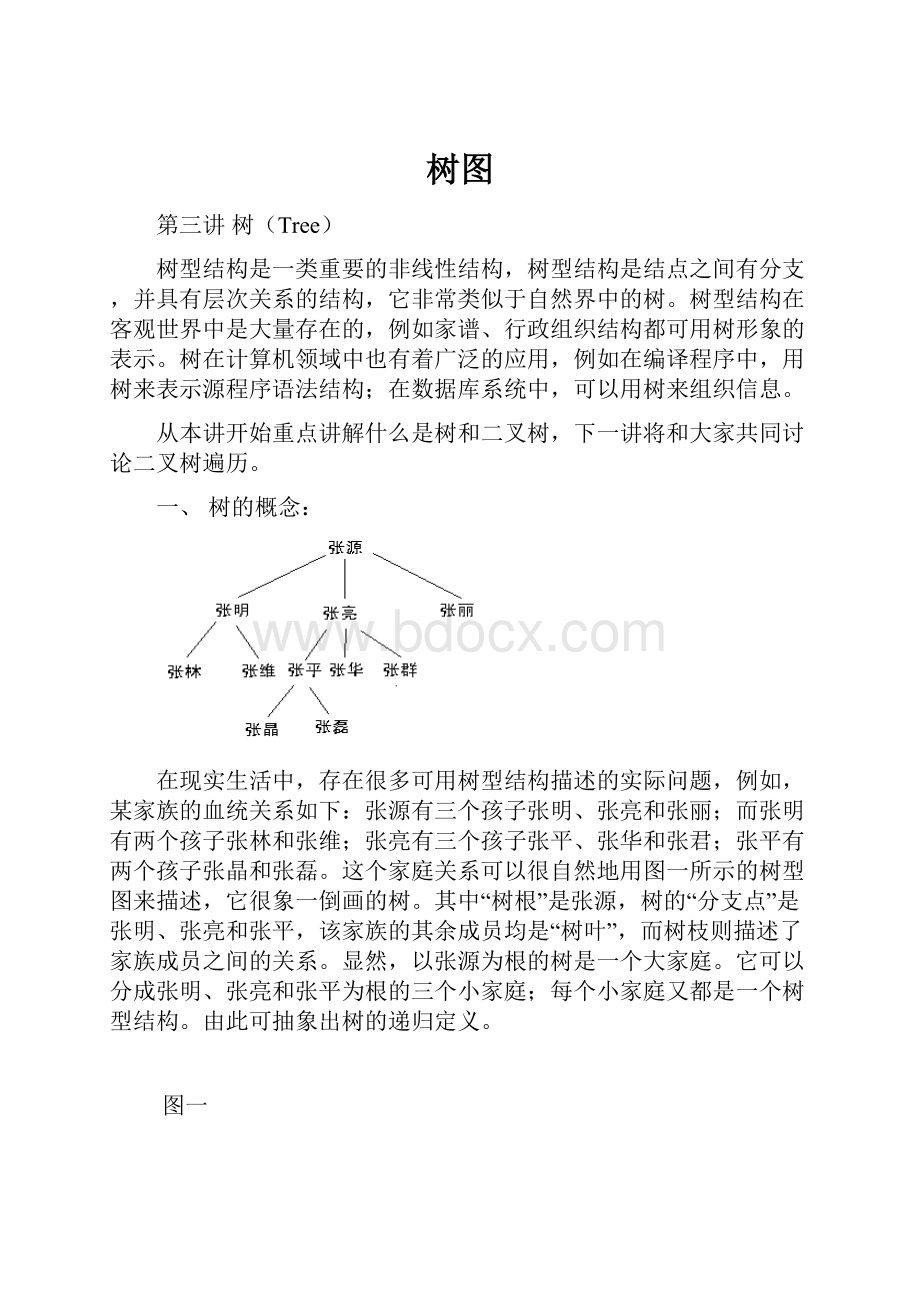
在现实生活中，存在很多可用树型结构描述的实际问题，例如，某家族的血统关系如下：

张源有三个孩子张明、张亮和张丽；而张明有两个孩子张林和张维；张亮有三个孩子张平、张华和张君；张平有两个孩子张晶和张磊。

这个家庭关系可以很自然地用图一所示的树型图来描述，它很象一倒画的树。

其中“树根”是张源，树的“分支点”是张明、张亮和张平，该家族的其余成员均是“树叶”，而树枝则描述了家族成员之间的关系。

显然，以张源为根的树是一个大家庭。

它可以分成张明、张亮和张平为根的三个小家庭；每个小家庭又都是一个树型结构。

由此可抽象出树的递归定义。

图一

定义：

树（Tree）是n（n＞0）个结点的有限集合T，它满足如下两个条件：

（1）、有且仅有一个特定的称为根（Root）的结点；

（2）、其余的结点可分为m（m≥0）个互不相交的有限集合T1，T2，…，Tm，其中每个集合又是一棵树，并称其为根的子树（Subtree）。

注意：

有的文献为了方便，也将n＝0的空集合定义为空树。

在树的树型图表示中，结点通常是用圆圈表示的，结点名字一般是写在圆圈旁边见图二，有时也可以写在圆圈内。

树的递归定义刻化树的固有特性，即一种树是由若干棵子树构成的，而子树又可由若干棵更小的子树构成。

用该定义来分析图二所示的树，它是由结点有限集T＝｛A，B，C，D，E，F，G，H，I，J｝所构成。

其中A是根结点，T中其余结点，可分成三个互不相交的子集；T1＝｛B，E，F，I，J｝，T2＝｛C｝，T3＝｛D，G，H｝；T1，T2和T3是根结点A的三棵子树，且本身又都是一棵树，例如T1，其根为B，其余结点可分为两个互不相交的子集T11＝｛E｝和T12＝｛F，I，J｝，它们都是B的子树。

T11是只含有一个根结点E的树；而T12的根F有两棵互不相交的子树｛I｝和｛J｝，其本身有都是只含有一个结点的树。

对T1和T3也可以进行类似的分析。

（a）树型表示法（b）集合表示法

图二

下面给出树结构中常用的基本术语，其中有许多术语借用了家族树中的一些习惯用词。

一个结点的子树个数称为该结点的度（Degree）。

一棵树的度是指该树中结点最大度数。

度为零的结点称为叶子（Leaf）或终端结点。

如图二中，A、B、E的度分别为3、2、0。

树的度为3，C、E、G、H、I和J均为叶子。

度不为零的结点或非终端结点，除根据结点之外的分支结点统称为内部结点。

树中某个结点子树之根称为该结点孩子（Child）或儿子，相应地，该结点称为孩子的双亲（Parents）或父亲。

如图二中，B是结点A的子树T1的根，故B是A的孩子，而A是B的双亲。

同一个双亲的孩子称为兄弟（Sibling）。

如图二中，B、C、D互为兄弟。

若树中存在一个结点序列k1，k2，…，kj，使得ki是ki+1的双亲（1≤i

路径的长度等于j-1，它是该路径所经过的边（即连接两个结点的线段）的数目。

由路径的定义可知，若一个结点序列是路经，则在树的树型图表中，该结点序列“自上而下”地通过路径上的每条边。

例如，在图二中，结点A到I有一条路径ABFI，它的长度为3。

显然，从树的根结点到树中其余结点均存在一条路径。

但是结点B和G之间不存在路径，因为既不可能从B点出发“自上而下”地经过若干结点到达G，也不可能从G出发“自上而下”地经过若干结点到达B。

若树中结点k到ks存在一条路径，则称k是ks祖先（Ancestor），ks是k的子孙（Descendant）。

显然，一个结点的祖先是从根结点到该结点路径上所经过的所有结点，而一个结点的子孙则是以该结点为根的子树中所有的结点。

我们约定：

结点k的祖先和子孙不包含结点k本身。

例如，在图二所示的树中，F的祖先是A和B，F的子孙是I和J。

结点的层数（Level）是从根开始算起的。

设根结点的层数为1，其余结点的层数等于其双亲点的层数加1。

例如在图二中，A的层数为1，B、C、D的层数2，E、F、G、H的层数为3，I和J的层数为4。

树中结点的最大层数称为树的高度（Height）或深度（Depth）。

如图二中树的高度为4。

若将树中每个结点的各子树看成是从左到右次序的（即不能互换），则称该树为有序树（OrderedTree）；否则称为无序树（UnordedTree）。

作为有序树，图三中的两棵树是不同的，因为结点A的两个孩子在两棵树中的左右次序不同。

在以后的讲解中，若不特别指明，我们所研究的树都是有序树。

图三

森林（Forest）是m（m≥0）棵互不相交的树的集合。

树和森林的概念很相近，删去一棵树的根，就得到一个森林。

反之，加上一个结点作树根，森林就变为一棵树。

树型结构的逻辑特征可用树中结点之间的父子关系来描述：

树中任一结点都可以有零个或多个后继（即孩子）结点，但至多只能有一个前驱（即双亲）。

树中只有根结点无前驱，叶结点无后继。

父子关系是非线性的，故树型结构是非线性结构。

祖先与子孙的关系是对父子关系的延拓，它定义了树中结点的纵向次序。

有序树的定义使得同一组兄弟结点之间是从左到右有长幼之分的。

如果对这一关系加以延拓，规定若k1和k2是兄弟，且k1在k2的左边，则k1的任一子孙都在k2的任一子孙的左边，那么我们就定义了树中结点的横向次序。

二、什么是二叉树

二叉树是树型结构的一个重要类型，许多实际问题抽象出来的数据结构往往是二叉树的形式，即使是一般的树也能简单地转换为二叉树，而且二叉树的存储结构及其算法都较为简单，因此，二叉树显得特别重要。

定义：

二叉树（BinaryTree）是（n≥0）个结点的有限集，它或者是空集（n＝0），或者由多个根结点及两棵互不相交、分别称作这个根的左子树和右子树的二叉树组成。

这也是一个递归定义。

二叉树可以是空集，因此，根可以有空的左子树或右子树，或者左右子树皆为空。

因此，二叉树有五种基本形态，如下图所示。

二叉树中，每个结点最多只能有两棵子树，并且有左右之分。

显然，它与无序树不同。

其实它与度数为2的有序树也不同，这是因为在有序树中，虽然一个结点的孩子之间是有左右次序的，但是若该结点只有一个孩子，就无须区分其左右次序。

而在二叉树中，即使是一个孩子也有左右之分。

例如，图五中（A）和（B）是两棵不同的二叉树，虽然它们同图六中的普通树（作为有序树或无序树）很相似，但是它们却不能等同于这棵普通树。

若将这棵树均看做普通树，则它们就是相同的了。

图五图六

由此可见，二叉树并非是树的特殊情形，尽管二者有许多相似之处，但它们是两种不同的数据结构。

遍历概念

所谓遍历（Traversal）是指沿着某条搜索路线，依次对树中每个结点均做一次且仅做一次访问。

访问结点所做的操作依赖于具体的应用问题。

遍历是二叉树上最重要的运算之一，是二叉树上进行其它运算之基础。

遍历方案

1．遍历方案

从二叉树的递归定义可知，一棵非空的二叉树由根结点及左、右子树这三个基本部分组成。

因此，在任一给定结点上，可以按某种次序执行三个操作：

（1）访问结点本身（N），

（2）遍历该结点的左子树（L），

  　（3）遍历该结点的右子树（R）。

以上三种操作有六种执行次序：

  　NLR、LNR、LRN、NRL、RNL、RLN。

  注意：

前三种次序与后三种次序对称，故只讨论先左后右的前三种次序。

2．遍历的命名

根据访问结点操作发生位置命名：

　　①NLR：

前序遍历（PreorderTraversal）

 ——访问结点的操作发生在遍历其左右子树之前。

②LNR：

中序遍历（InorderTraversal）

 ——访问结点的操作发生在遍历其左右子树之中（间）。

③LRN：

后序遍历（PostorderTraversal）

 ——访问结点的操作发生在遍历其左右子树之后。

④层次遍历，又叫宽度优先遍历，即一层一层，从左到右的访问所有节点。

注意：

  　由于被访问的结点必是某子树的根，所以N（Node）、L（Leftsubtlee）和R（Rightsubtree）又可解释为根、根的左子树和根的右子树。

NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。

遍历序列

1．遍历二叉树的执行踪迹

  　三种递归遍历算法的搜索路线相同（如下图虚线所示）。

具体线路为：

  　从根结点出发，逆时针沿着二叉树外缘移动，对每个结点均途径三次，最后回到根结点。

2．遍历序列

（1）中序序列

  中序遍历二叉树时，对结点的访问次序为中序序列

　【例】中序遍历上图所示的二叉树时，得到的中序序列为：

          DBAECF

（2）先序序列

  先序遍历二叉树时，对结点的访问次序为先序序列

  【例】先序遍历上图所示的二叉树时，得到的先序序列为：

          ABDCEF

（3）后序序列

  　后序遍历二叉树时，对结点的访问次序为后序序列

　【例】后序遍历上图所示的二叉树时，得到的后序序列为：

          DBEFCA

  注意：

（1）在搜索路线中，若访问结点均是第一次经过结点时进行的，则是前序遍历；若访问结点均是在第二次（或第三次）经过结点时进行的，则是中序遍历（或后序遍历）。

只要将搜索路线上所有在第一次、第二次和第三次经过的结点分别列表，即可分别得到该二叉树的前序序列、中序序列和后序序列。

（2）上述三种序列都是线性序列，有且仅有一个开始结点和一个终端结点，其余结点都有且仅有一个前趋结点和一个后继结点。

为了区别于树形结构中前趋（即双亲）结点和后继（即孩子）结点的概念，对上述三种线性序列，要在某结点的前趋和后继之前冠以其遍历次序名称。

【例】上图所示的二叉树中结点C，其前序前趋结点是D，前序后继结点是E；中序前趋结点是E，中序后继结点是F；后序前趋结点是F，后序后继结点是A。

但是就该树的逻辑结构而言，C的前趋结点是A，后继结点是E和F。

图的定义与术语

图（G）是一种比线性表和树结构更复杂的数据结构，是非线性的数据结构，应用非常广泛。

图：

图G由两个集合V（G）和E（G）组成，记为：

G=（V，E）。

其中，V（G）是顶点的非空有限集合，E（G）是边的有限集合，边是顶点的无序对或有序对。

有向图：

若E（G）是有向边（也称为弧）的有限集合时，则为有向图。

弧是顶点的有序对，记为，其中V、W是顶点，V称为弧尾，W称为弧头。

我们说是从顶点V到顶点W的弧，也可说顶点W和顶点V相邻，或V邻接W。

无向图：

若E（G）是无向边（简称边）的有限集合时，则为无向图。

边是顶点的无序对，记为（V，W）或（W，V），因为（V，W）=（W，V），其中V、W是顶点。

我们说（V，W）是V邻接W，或W邻接V。

例：

有向图G1和无向图G2

图G1有

V（G1）={1，2，3，4，5，6}

E（G1）={<1，2>，<2，1>，<2，3>，<2，4>，<3，5>，<5，6>，<6，3>}

图G2有

V（G2）={1，2，3，4，5，6，7}

E（G2）={（1，2），（2，3），（3，1），（2，4），（2，5），（5，6），（5，7）}

完备图无向图：

对一个有n个顶点的无向图，若每个顶点到其它（n-1）个顶点都连有一条边，则图中共有n（n-1）/2条边。

完备图有向图：

对一个有n个顶点的有向图，若任何两顶点都有方向相反的两条弧连接，则图中共有n（n-1）条弧。

权：

若图上的每条边有一相应的数值，这个数值就叫该边的权。

这种图一般叫做网络。

路径：

在一个图中，若从顶点V1出发，沿一些边经过顶点V2，V3，...，Vn-1到达顶点Vn，则成顶点序列（V1，V2，...，Vn-1，Vn）为从V1到Vn的路径。

对于有向图，路径也是有向的，路径的方向是由起点到终点且需与它经过的每条边的方向一致。

路径长度：

沿此路径上边的数目为路径长度；对有权的图，一般取沿路径各边的权之和作为此路径的长度。

简单路径：

如果一条路径上的所有顶点，除起始顶点和终止顶点外，都是彼此不同的，则可说该路径是一条简单路径。

简单回路：

如果一条简单路径，其长度2，且路径起始和结束在同一顶点上，则说该路径是一个简单回路。

单向连通：

若从顶点V到顶点W有一条路径，则说V到W是单向连通，或称连通的。

连通图：

如果图G中任意两个顶点都是连通的，则说G是一个连通图。

非连通图的每一个连通部分叫连通分量。

强连通图：

对于有向图，若从顶点Vi到顶点Vj和从顶点Vj到顶点Vi之间都有路径，则称这两个顶点是强连通的。

若图中任何一对顶点都是强连通的，则称此图为强连通图。

非强连通图的每一个强连通部分叫强连通分量。

度：

与每个顶点相连的边数，称为该顶点的度。

对于有向图，顶点的度有入度和出度之区别，以顶点V为头的弧的数目称为V的入度，以顶点V为尾的弧的数目称为V的出度。

子图：

设G=（V，E）和G'=（V'，E'）是两个有向图，如果有V'V，E'E，则说G'是G的子图。